历史记录

清除记录

猜你想搜

AcWing热点
App
登录/注册

AcWing 1020. 潜水员【01背包问题+二维费用'不少于'问题】原题链接简单

作者：

一只野生彩色铅笔 , 2021-06-20 17:00:47 , 所有人可见 , 阅读 5371

72

15

最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

一共有 $k$ 种物品，对于第 $i$ 种物品，第一维费用是 $v_{1i}$，第二维费用是 $v_{2i}$，价值是 $w_i$

每个物品只能 被选一次

求一个 选择方案，使得第一维费用 不少于 $n$，第二维费用 不少于 $m$ 且 总价值最小

分析

本题是一个 二维费用01背包问题 ，但和一般的 二维费用01背包问题 不同

这题要求的是 费用不少于 规定条件，因此我们需要对于 状态的定义 进行改变

具体直接参考以下 闫氏DP分析法

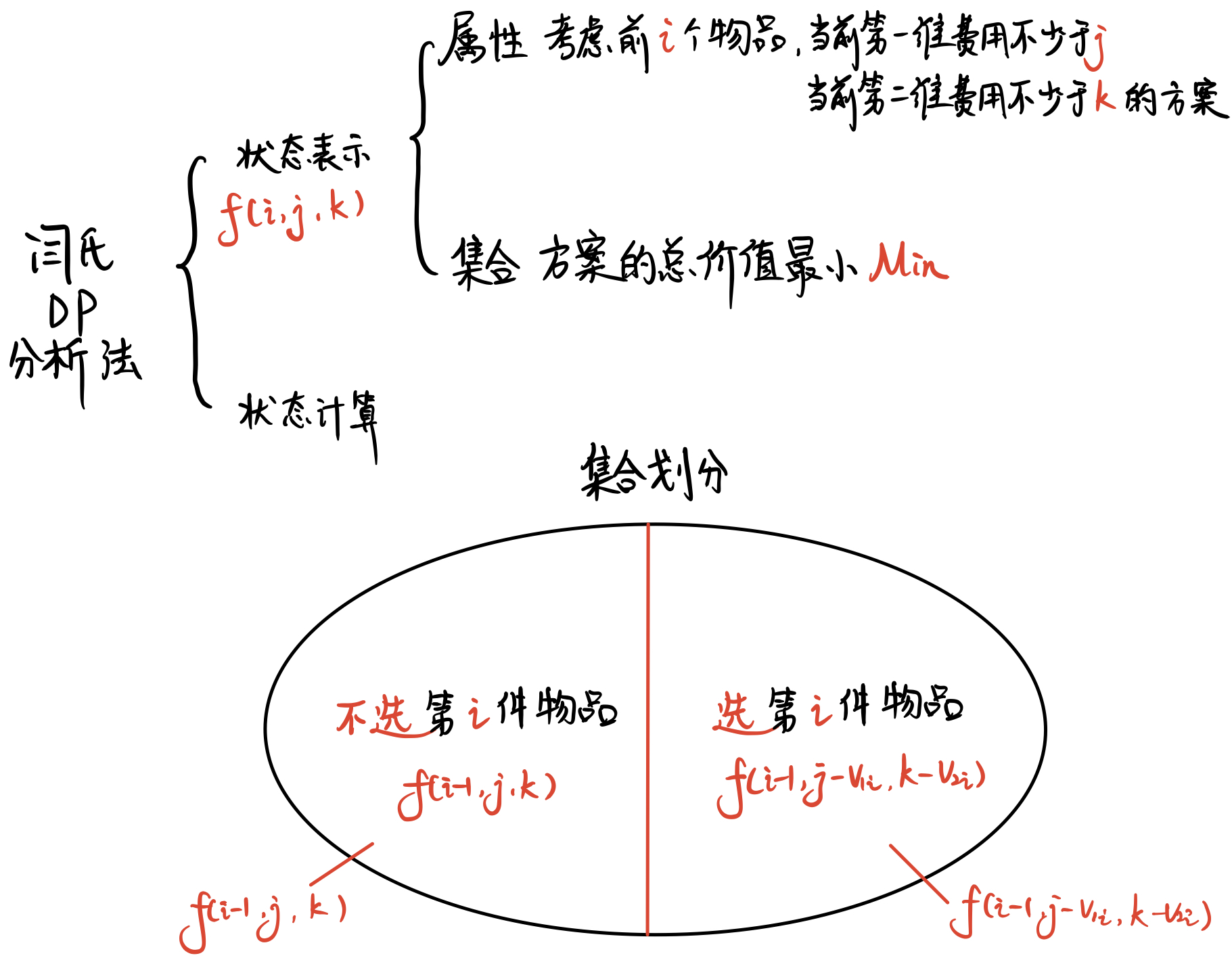
初始状态：f[0][j][k] $\quad 其中~j,k\le 0$

目标状态：f[k][n][m]

Code

时间复杂度： $O(k \times n \times m)$

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, M = 85;

int n, m, t;

int v1[N], v2[N], w[N];
int f[M][M];

int main()
{
    cin >> n >> m >> t;
    for (int i = 1; i <= t; ++ i) cin >> v1[i] >> v2[i] >> w[i];

    memset(f, 0x3f, sizeof f); //求最小值要把除初始状态以外的所有状态初始化为+∞
    f[0][0] = 0; //这里我们把所有j,k小于0的初始状态都合并到f[0][0][0]中来转移,也就是下面的max操作
    for (int i = 1; i <= t; ++ i)
    {
        for (int j = n; j >= 0; -- j)
        {
            for (int k = m; k >= 0; -- k)
            {
                f[j][k] = min(f[j][k], f[max(j - v1[i], 0)][max(k - v2[i], 0)] + w[i]);
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

24 评论

zhangxc 2022-06-16 14:31

分析图里面选第i个物品的情况忘记加上第i个物品的价值了

Cplusplus 2023-04-30 19:43

……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

糖豆 2023-06-30 08:14

你是对的，我帮铅笔大佬改一下：

千世 6个月前

图里面的集合和属性反了吧

采石的山雀 6天前

确实是

William_50 2023-08-24 22:19

强！！！

3Q 2022-08-17 22:42

想问下为什么最后不用循环所有方案求最小值呢？(y总一开始的错误代码里面最后循环了一遍的原因是啥

安溥 2022-11-01 23:19

状态转移的时候已经自动min了

颓废 2023-03-25 13:29

两次的状态转移方程表示含义不一样

终末 2022-07-17 20:11

大佬借个图

gtt 2022-04-04 23:59

Orz

我是憨憨一号 2021-11-21 17:50

真的牛批

种花家的小兔子 2021-11-12 00:00

聚聚当前这个dp的初始化假设是最最朴素的版本，f[i][[j][k]那种的, 是不是只用初始化f[0][j][k]就可以了？
f[0][0][0] = 0, 其他f[0][j][k]都是INF

一只野生彩色铅笔 2021-11-12 17:50

应该是的

糖豆 2023-06-30 08:15

最朴素的代码是这样的：

#include <bits/stdc++.h>

using namespace std;
const int N = 1010;
const int M = 110;
int f[N][M][M];
int n, m1, m2;

//二维费用01背包-不少于维度费用，求最小代价
int main() {
    //注意次序
    scanf("%d %d %d", &m1, &m2, &n);
    //求最小值
    memset(f, 0x3f, sizeof f);
    f[0][0][0] = 0;

    for (int i = 1; i <= n; i++) {
        int v1, v2, w;
        scanf("%d %d %d", &v1, &v2, &w);
        for (int j = 0; j <= m1; j++)
            for (int k = 0; k <= m2; k++) {
                //不选择i号物品
                f[i][j][k] = f[i - 1][j][k];
                //分情况讨论

                //物品i加上就够一维使用，此时，只关心二维情况即可
                if (j - v1 < 0 && k - v2 >= 0)
                    f[i][j][k] = min(f[i][j][k], f[i - 1][0][k - v2] + w);
                //物品i加上就够二维使用，此时，只关心一维情况即可
                else if (j - v1 >= 0 && k - v2 < 0)
                    f[i][j][k] = min(f[i][j][k], f[i - 1][j - v1][0] + w);
                //如果选择了i号物品，两个维度直接拉满，那么只选择一个i就足够用，它参选的价值是w
                else if (j - v1 < 0 && k - v2 < 0)
                    f[i][j][k] = min(f[i][j][k], w);
                else
                    //正常递推
                    f[i][j][k] = min(f[i][j][k], f[i - 1][j - v1][k - v2] + w);
            }
    }
    printf("%d\n", f[n][m1][m2]);
    return 0;
}