最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

有 $n$ 件物品 和 一个容量为 $V$ 的背包，背包最大承重是 $M$

每件物品只能 用一次，第 $i$ 件物品的 体积 是 $v_i$，重量 是 $m_i$，价值 是 $w_i$

求解一个选物品的 方案，使得 总体积 不超过 $V$，总重量 不超过 $M$ 的，且 总价值 最大

分析

每件物品只能 用一次 因此是个 01背包模型

费用一共有两个，一个是 体积，一个是 重量，因此是个 01背包二维费用问题

本题是一道裸题，直接上 闫氏DP分析法

闫氏DP分析法

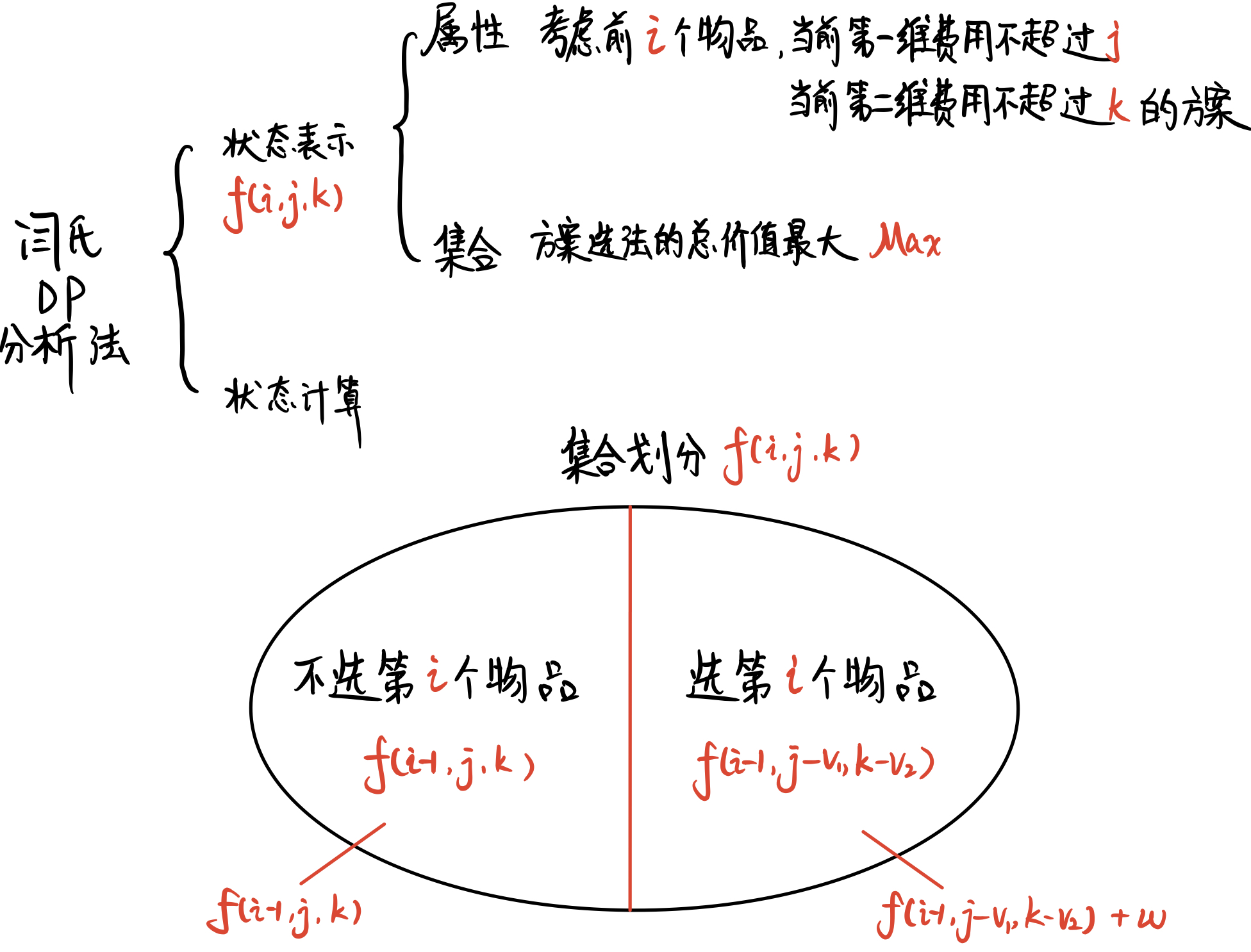
初始状态：f[0][0][0]

目标状态：f[n][V][M]

Code

时间复杂度 ：$O(n\times v_1\times v_2)$

空间复杂度 ：$O(v_1\times v_2)$

#include <iostream>

using namespace std;

const int N = 1010, K = 110;

int n, V, M;

int v1[N], v2[N], w[N];
int f[K][K];

int main()
{
    //input
    cin >> n >> V >> M;
    for (int i = 1; i <= n; ++ i) cin >> v1[i] >> v2[i] >> w[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = V; j >= v1[i]; -- j)
        {
            for (int k = M; k >= v2[i]; -- k)
            {
                f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + w[i]);
            }
        }
    }
    //output
    cout << f[V][M] << endl;
    return 0;
}