最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

有 $n$ 种物品和一个 容量 为 $m$ 的背包

物品分三类：

1. 第一类物品只能用 $1$ 次（01背包）；
2. 第二类物品可以用无限次（完全背包）；
3. 第三类物品最多只能用 $s_i$ 次（多重背包）；

每种体积是 $v_i$，价值是 $w_i$

求解一个选物品的方案，是的物品 总体积 不超过背包的 容量，且 总价值最大

分析

该题就是一道 混合背包 的裸题

结合每个 物品 的属性，分别做不同的 状态转移 即可

可以结合 01背包、完全背包、多重背包 这三篇博客配套使用

此处的多重背包还要采用 二进制优化 变成多个 01背包 来做，不然会卡 TLE

闫氏DP分析法

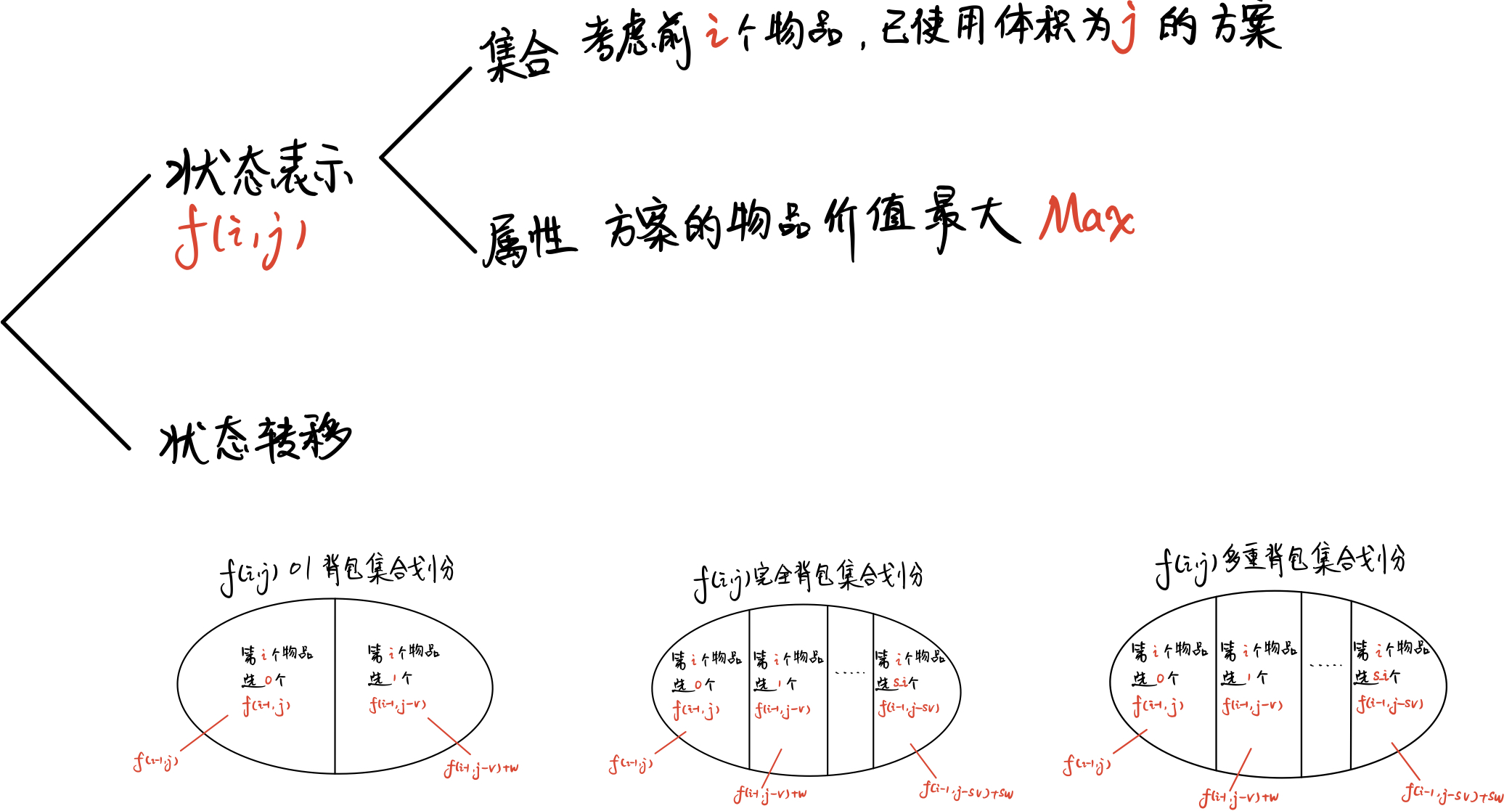
Code

时间复杂度：$O(n \times m \times \log s)$

空间复杂度：$O(m)$

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N], s[N];
int f[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; ++ i)
    {
        //完全背包
        if (!s[i])
        {
            for (int j = v[i]; j <= m; ++ j)
            {
                f[j] = max(f[j], f[j - v[i]] + w[i]);
            }
        }
        else
        {
            //把多重背包用二进制优化
            //这样就变成做多个01背包了
            if (s[i] == -1) s[i] = 1;
            //二进制优化
            for (int k = 1; k <= s[i]; k *= 2)
            {
                for (int j = m; j >= k * v[i]; -- j)
                {
                    f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
                }
                s[i] -= k;
            }
            if (s[i])
            {
                for (int j = m; j >= s[i] * v[i]; -- j)
                {
                    f[j] = max(f[j], f[j - s[i] * v[i]] + s[i] * w[i]);
                }
            }
        }
    }

    cout << f[m] << endl;

    return 0;
}