最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

一共有 $n$ 种奖品，$m$ 元现金

对于第 $i$ 种奖品，其 价格 为 $v_i$，价值 为 $w_i$，数量 为$s_i$

制定一个购买 方案，使得该方案的总价值 最大

分析

物品个数为 $n$，总体积为$m$，初步识别是一个 背包问题

观察到每个物品有 数量限制，断定该题是 多重背包问题

本题是一道 多重背包 的裸题

本篇题解，只展示 多重背包 的朴素优化和分析，关于 单调队列优化 可以看这篇博客
AcWing 6. 多重背包问题 III【单调队列优化+图示】

不多废话，我们直接上 闫氏DP分析法

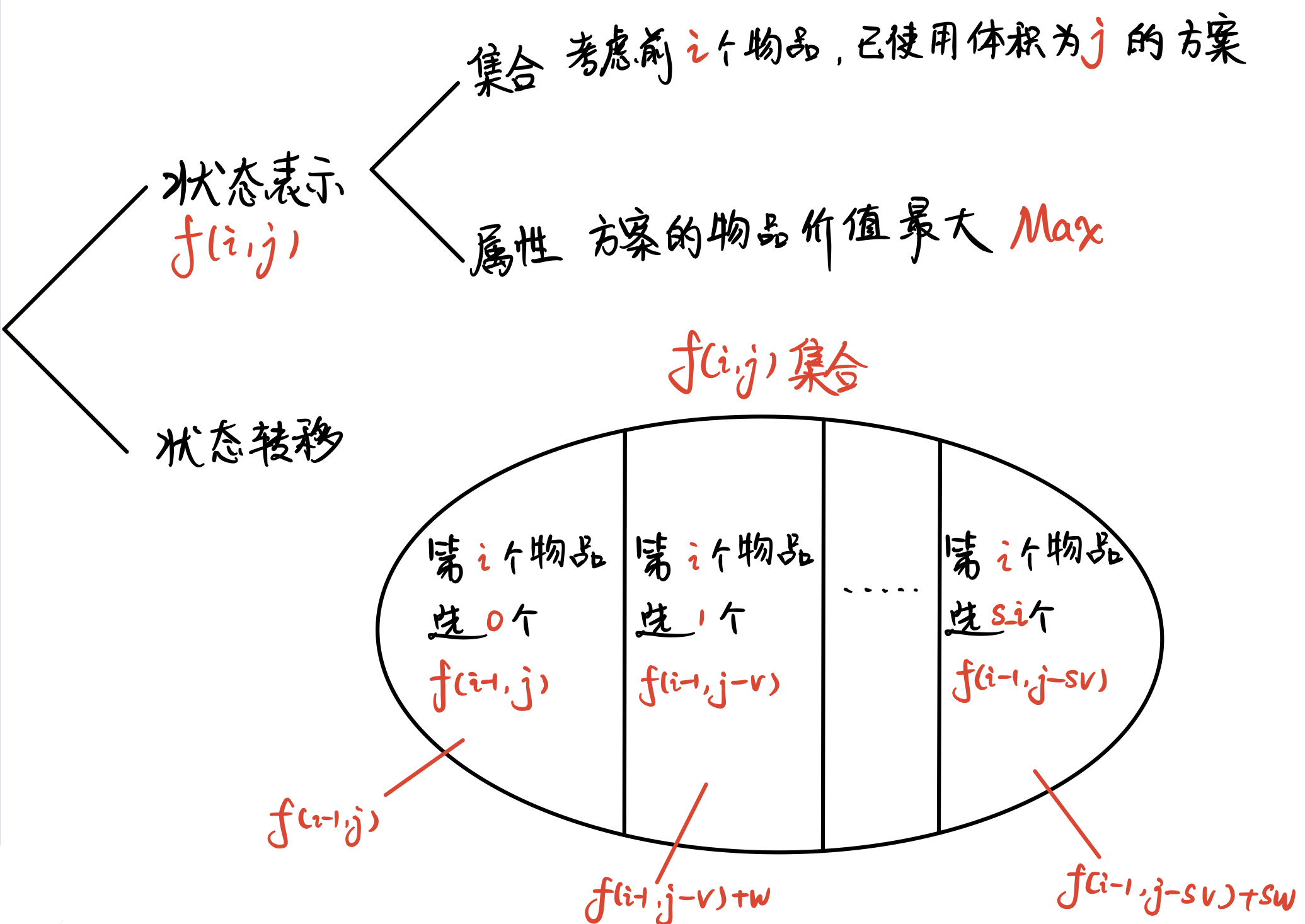
闫氏DP分析法

初始状态：f[0][0]
目标状态：f[n][m]

Code(朴素写法)

时间复杂度：$O(n \times m \times s)$

空间复杂度：$O(n \times m)$

#include <iostream>

using namespace std;

const int N = 510, M = 6010;

int n, m;
int v[N], w[N], s[N];
int f[N][M];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= m; ++ j)
        {
            for (int k = 0; k <= s[i]; ++ k)
            {
                if (j - k * v[i] >= 0)
                {
                    f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                }
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

朴素优化方式

同 01背包 ，对于第 i 阶段的状态更新只会用到第 i-1 阶段的状态

因此可以采用 滚动数组 或者根据状态更新的顺序，直接压缩成 一维 的优化方式

时间复杂度：$O(n \times m \times s)$

空间复杂度：$O(m)$

一维优化方式

#include <iostream>

using namespace std;

const int N = 510, M = 6010;

int n, m;
int v[N], w[N], s[N];
int f[M];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = m; j >= v[i]; -- j)
        {
            for (int k = 0; k <= s[i]; ++ k)
            {
                if (j - k * v[i] >= 0)
                {
                    f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
                }
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}