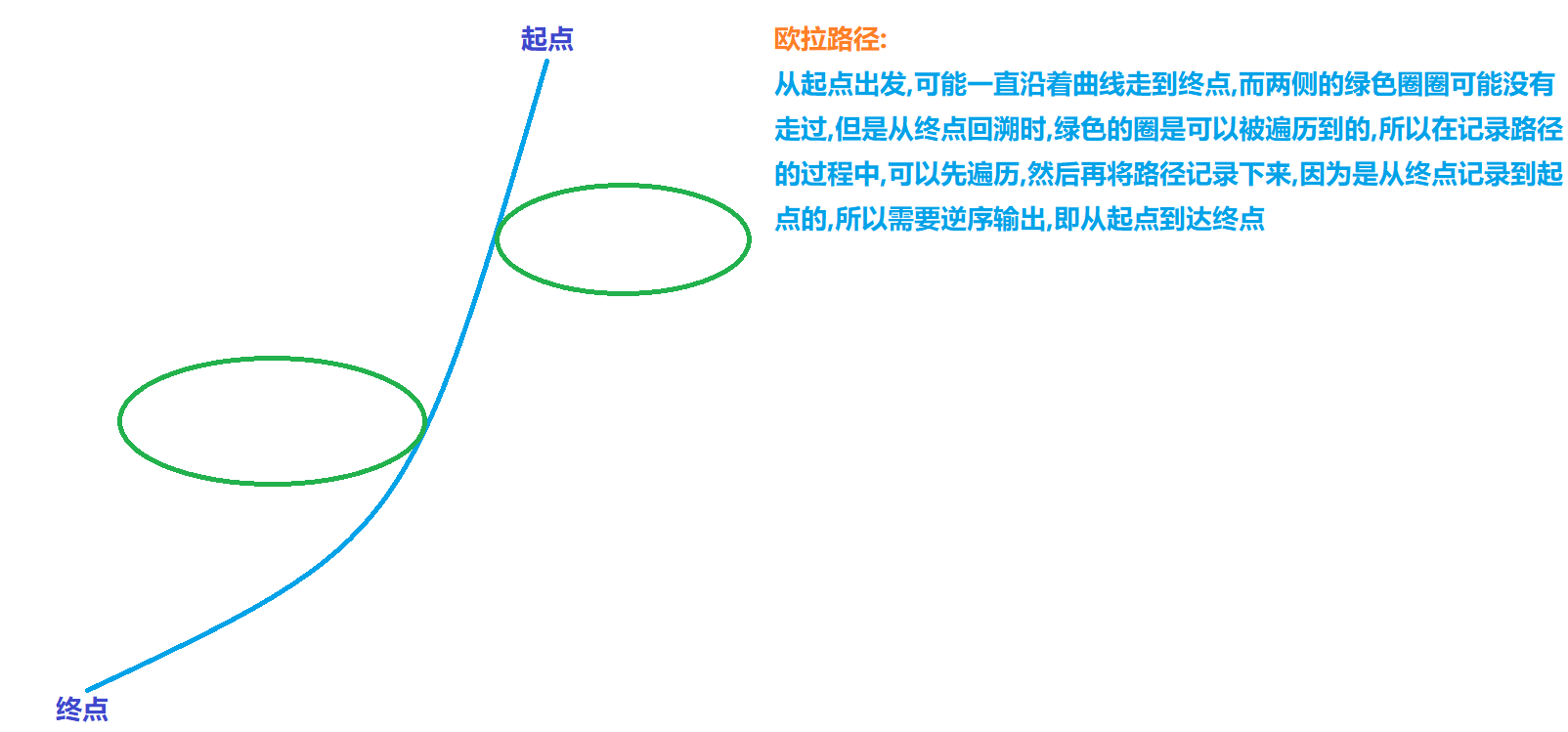
遍历过程中的注意事项;

边的转化

无向图中的边的序号为:0~2m-1,而在题目中的编号是1~m;
所以转化边时:0,1对应1号边,2,3对应2号边,即x号边对应x/2+1
其中偶数是正向边,奇数是反向边,可以用x^1转化正反向边的关系;
如果是奇数:x^1中,x二进制前面的数不变,最后一位变成0,即x^1=x-1;
如果是偶数:x^1中,x二进制前面的数不变,最后一位变成1,即x^1=x+1;

#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N=100010,M=400010;

int ans[M/2],cnt;//ans表示欧拉路径,cnt表示路径上边的数量
int h[N],ne[M],e[M],idx;
bool used[M];
int din[N],dout[N];//点的出度与入度;
int type,n,m;

void insert(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void dfs(int u)
{
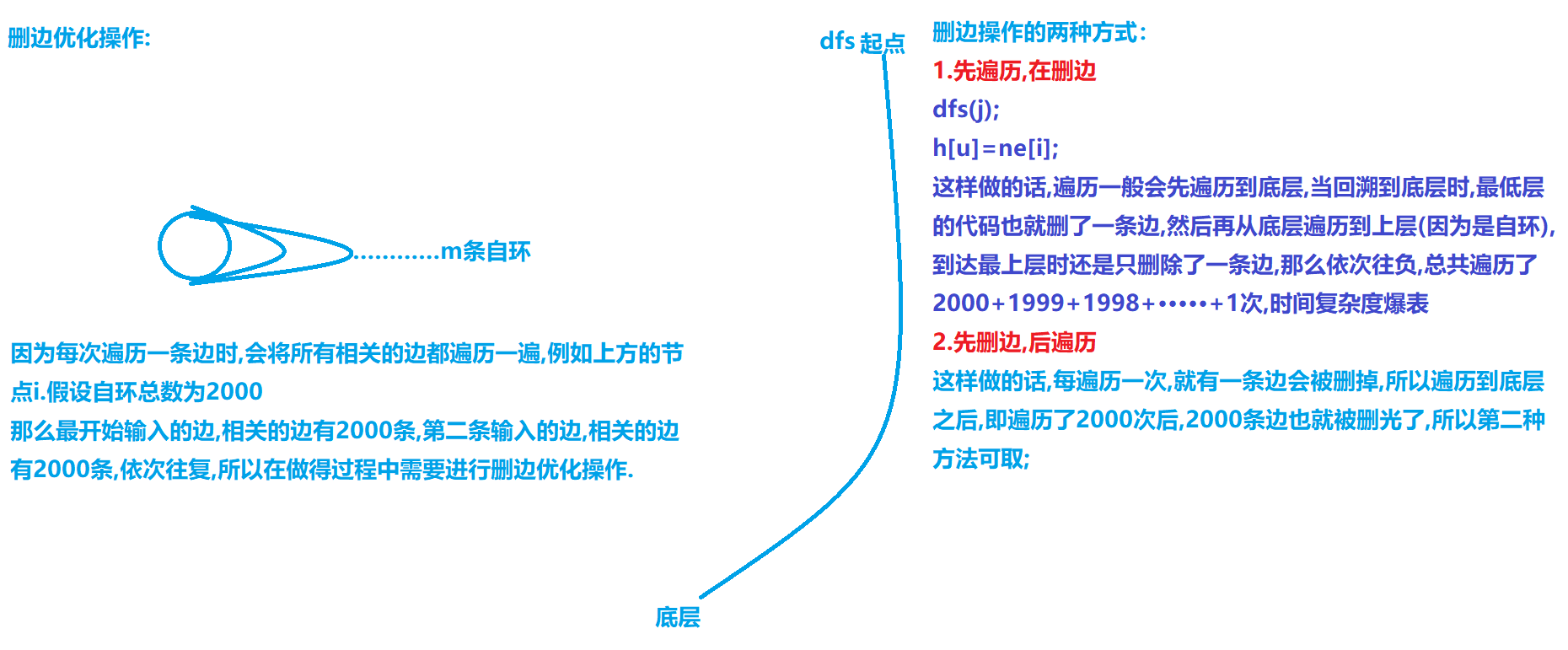
    for(int &i=h[u];~i;)//使用引用,可以直接在i=ne[i]中,将边删掉;
    {
        if(used[i])//如果该条边使用过了,就直接删去,可以防止再次遍历,从而降低复杂度
        {
            i=ne[i];
            continue;
        }

        used[i]=true;
        if(type==1) used[i^1]=true;//无向图中的反向边也标记一下;

        int t;
        if(type==1)
        {
            t=i/2+1;//转化为边的编号
            if(i&1) t=-t;//如果是反向边
        }
        else t=i+1;

        int j=e[i];
        i=ne[i];//边用过之后直接删了
        dfs(j);
        ans[++cnt]=t;//从下往上将点输入到路径中,因为从上往下的过程中,可能边路有些环并没有被顾虑到
    }
}

int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d%d",&type,&n,&m);

    for(int i=1;i<=m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        insert(a,b);
        dout[a]++,din[b]++;//记录入度和出度
        if(type==1) insert(b,a);
    }

    if(type==1)
    {
        for(int i=1;i<=n;i++)
        if(din[i]+dout[i]&1)//无向图欧拉回路中度数为奇数的点为0;
        {
            printf("NO");
            return 0;
        }
    }
    else 
    {
        for(int i=1;i<=n;i++)
        if(din[i]!=dout[i])//有向图欧拉回路中,入度与出度相同
        {
            printf("NO");
            return 0;
        }
    }

    for(int i=1;i<=n;i++)//找到一个不是孤立的点,即有边的点
    if(h[i]!=-1)
    {
        dfs(i);
        break;
    }

    if(cnt<m) //如果回路中的边数小于总边数,则不构成欧拉回路
    {
        printf("NO");
    }
    else//因为是逆序将点输入的,所以要逆序将点打出来;
    {
        printf("YES\n");
        for(int i=cnt;i>=1;i--)
        {
            printf("%d ",ans[i]);
        }
    }

    return 0;
}