导读：什么是最大匹配？
要了解匈牙利算法必须先理解下面的概念：
匹配：在图论中，一个「匹配」是一个边的集合，其中任意两条边都没有公共顶点。
最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。
下面是一些补充概念：
完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。
交替路：从一个未匹配点出发，依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。
增广路：从一个未匹配点出发，走交替路，如果途径另一个未匹配点（出发的点不算），则这条交替 路称为增广路（agumenting path）。
匈牙利算法
不讲算法证明(我也不会)。
用一个转载的例子来讲解匈牙利算法的流程。
代码实现匈牙利算法
首先是存图模板
//邻接表写法，存稀疏图
int h[N],ne[N],e[N],idx;
//n1,n2分别是两个点集的点的个数
int n1,n2,m;
void add(int a , int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void init()
{
memset(h,-1,sizeof h);
}
//存边只存一边就行了，虽然是无向图。
for(int i = 0 ; i < n1 ; i ++)
{
int a,b;
cin>>a>>b;
add(a,b);
}
接下来看算法模板(c++)
//match[j]=a,表示女孩j的现有配对男友是a
int match[N];
//st[]数组我称为临时预定数组，st[j]=a表示一轮模拟匹配中，女孩j被男孩a预定了。
int st[N];
//这个函数的作用是用来判断,如果加入x来参与模拟配对,会不会使匹配数增多
int find(int x)
{
//遍历自己喜欢的女孩
for(int i = h[x] ; i != -1 ;i = ne[i])
{
int j = e[i];
if(!st[j])//如果在这一轮模拟匹配中,这个女孩尚未被预定
{
st[j] = true;//那x就预定这个女孩了
//如果女孩j没有男朋友，或者她原来的男朋友能够预定其它喜欢的女孩。配对成功,更新match
if(!match[j]||find(match[j]))
{
match[j] = x;
return true;
}
}
}
//自己中意的全部都被预定了。配对失败。
return false;
}
//记录最大匹配
int res = 0;
for(int i = 1; i <= n1 ;i ++)
{
//因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
memset(st,false,sizeof st);
if(find(i))
res++;
}
下面用一个gif动图来演示这个整个配对的递归过程：
练习例题： 二分图的最大匹配
AC代码
#include<iostream>
#include<cstring>
using namespace std;
const int N = 510 , M = 100010;
int n1,n2,m;
int h[N],ne[M],e[M],idx;
bool st[N];
int match[N];
void add(int a , int b)
{
e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
void init()
{
memset(h,-1,sizeof h);
}
int find(int x)
{
//遍历自己喜欢的女孩
for(int i = h[x] ; i != -1 ;i = ne[i])
{
int j = e[i];
if(!st[j])//如果在这一轮模拟匹配中,这个女孩尚未被预定
{
st[j] = true;//那x就预定这个女孩了
//如果女孩j没有男朋友，或者她原来的男朋友能够预定其它喜欢的女孩。配对成功
if(!match[j]||find(match[j]))
{
match[j] = x;
return true;
}
}
}
//自己中意的全部都被预定了。配对失败。
return false;
}
int main()
{
init();
cin>>n1>>n2>>m;
while(m--)
{
int a,b;
cin>>a>>b;
add(a,b);
}
int res = 0;
for(int i = 1; i <= n1 ;i ++)
{
//因为每次模拟匹配的预定情况都是不一样的所以每轮模拟都要初始化
memset(st,false,sizeof st);
if(find(i))
res++;
}
cout<<res<<endl;
}
简单来说st的作用就是，避免女生j的现男友k去找备胎的时候，又去找到这个j
点了，清晰明了hhhh
明白了
谢谢，明白了
🐂
太对了！！！
hhhhh 懂了
图片：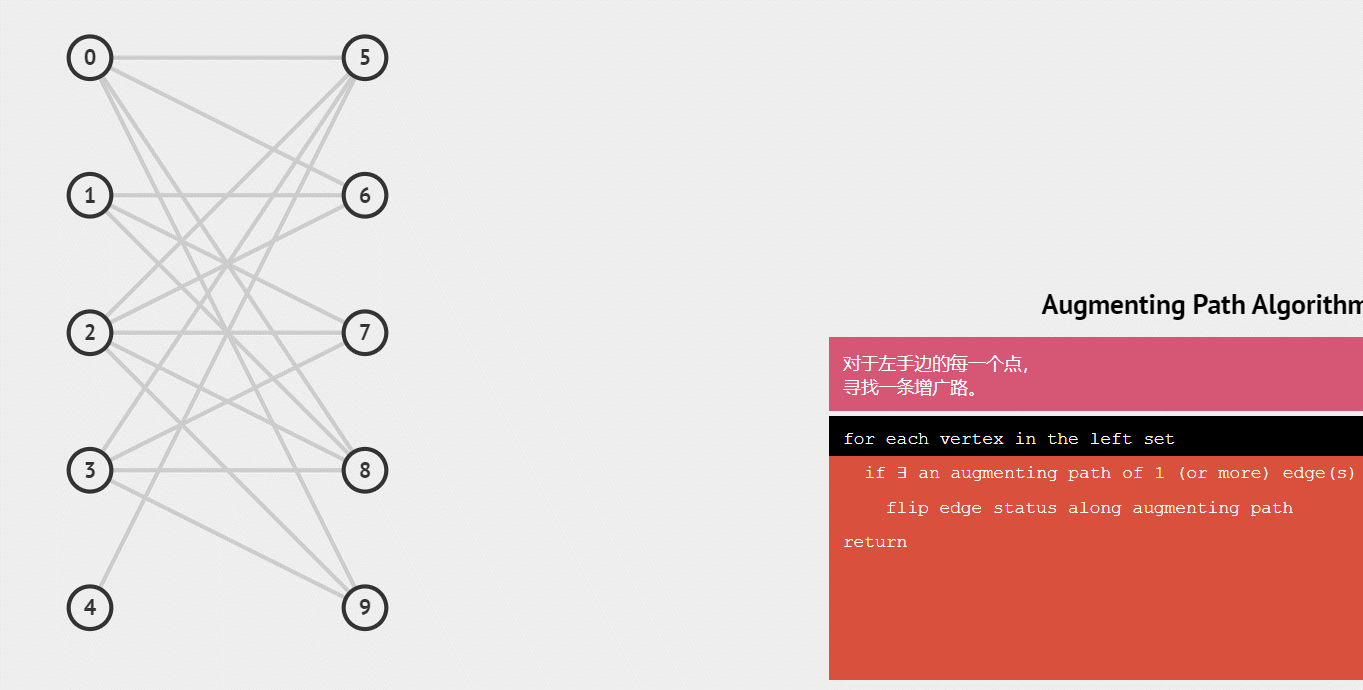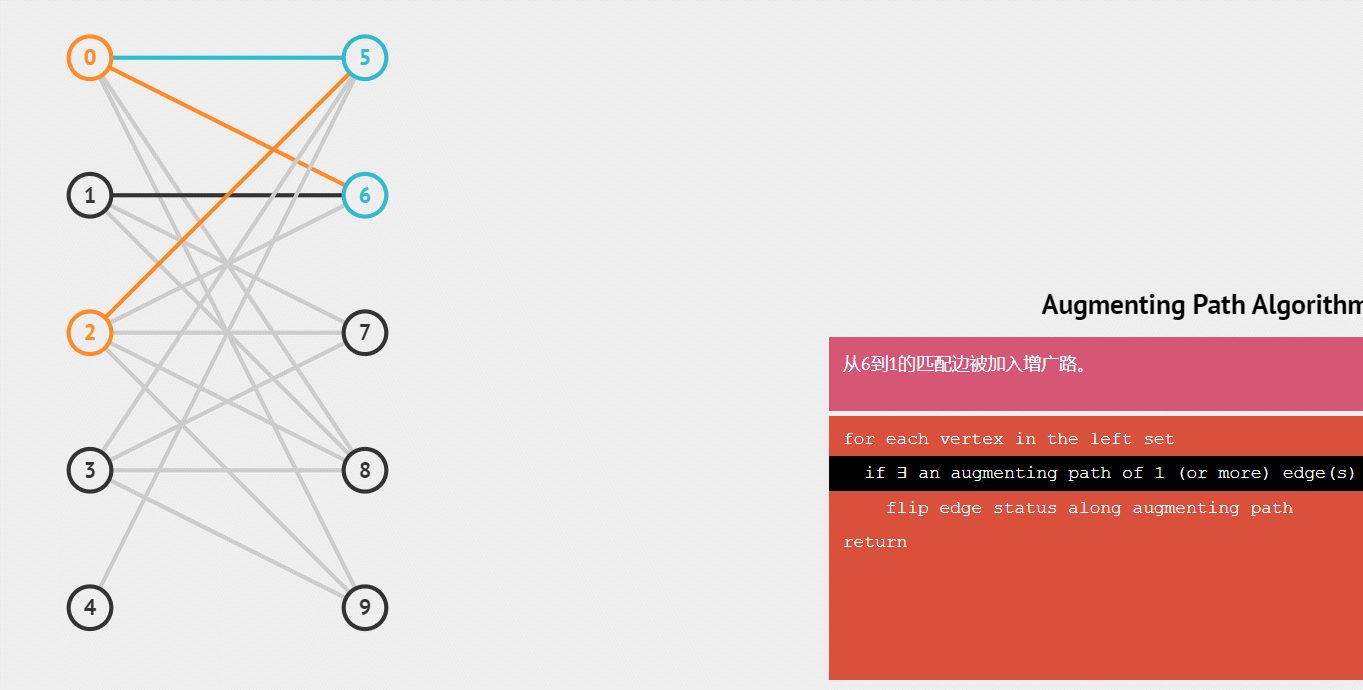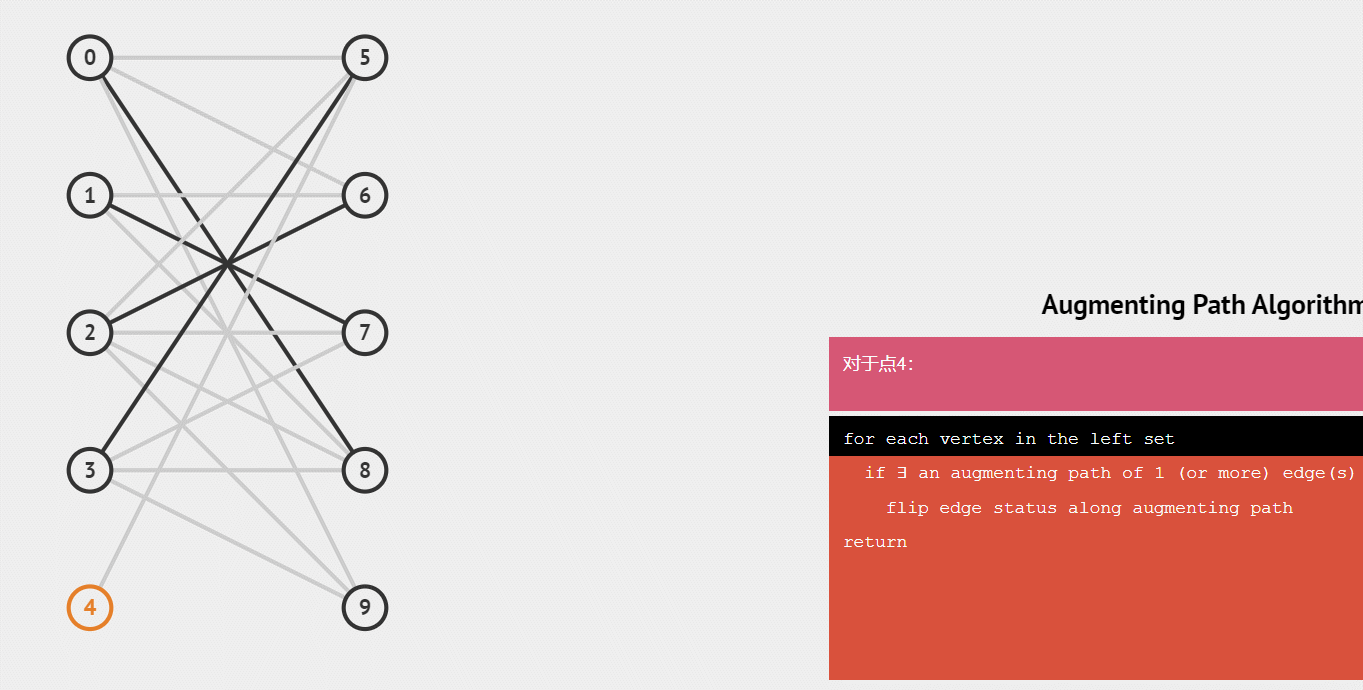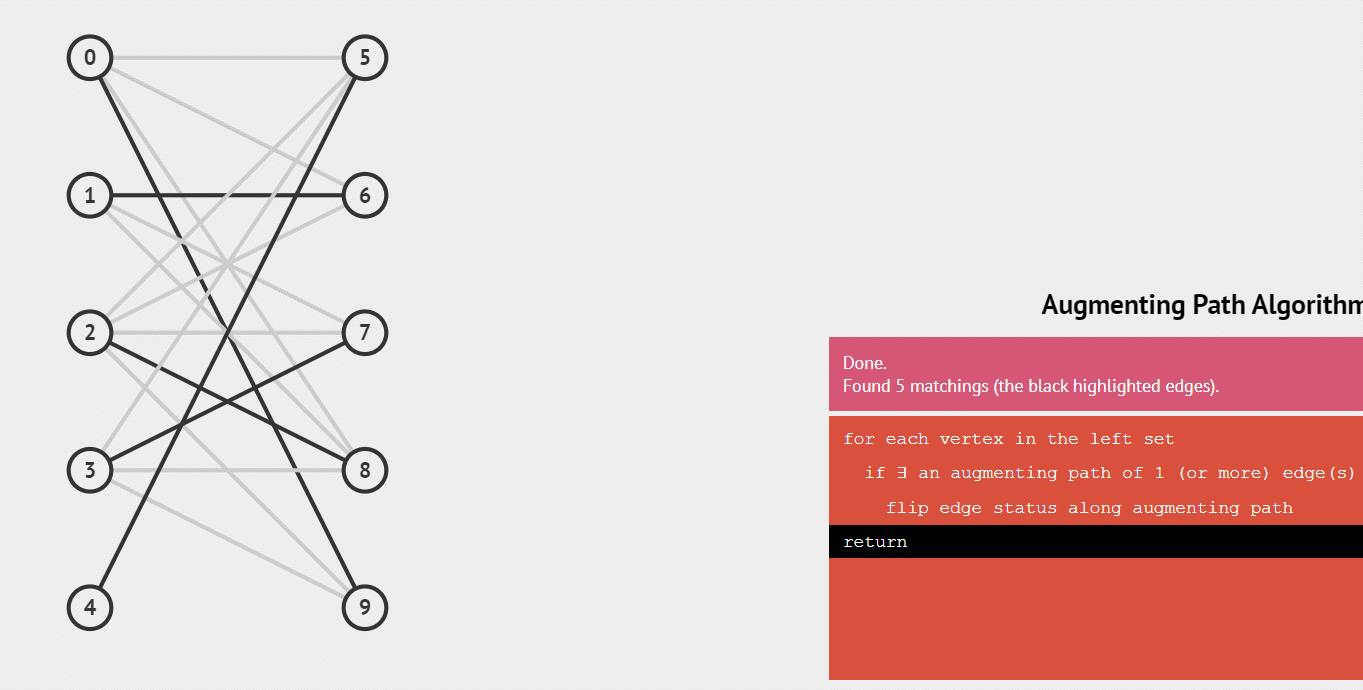
这个gif用什么做的呢?
原作者用这个gif动图(匈牙利算法.gif)来演示这个整个配对的递归过程，之前图挂了，现在是补链
好的好的，谢谢
visualgo.net NUS 做的算法可视化网站，有中文支持
好快啊o(╥﹏╥)o
优化一点点
至于为啥需要每轮重置st，感受一下这个样例
2 2 3
1 2
1 1
2 1
重置st是为了每次find搜索时避免重复搜索
这个是st的作用。重置是因为对于之前的一个点它相对于他走不通，但对于当前的点并于一定，所以要在重试一下这个点对于当前的点是否可行。
感谢你这一问，我一直没看到哪一行，一直在找为什么这个算法是正确的。。。
补充一下证明：
1) 匈牙利算法中，一个有伴侣的人，无论男女，不会重新变成单身。
2) 若我们尝试给一个有对象的女生换个对象，如果成功，整个交换链条终止于一个单身女性。
由2)可知，调整对象失败则代表由该女生作为起点的生成树内已无单身女性。
由1)可知，以该女生作为起点的生成树不会凭空出现单身女性。
大佬 牛 真正解答了我的疑惑
例子也很正确！
爱了爱了
那为什么不能回溯st[i] true分两种情况 保留无调整空间的true st就不用每轮刷新了
我感觉重置st的作用是让每个男生都可以无障碍地进行预定操作emmm
你这个证明太抽象了，我说一下我的理解，其实匈牙利算法隐藏了一个很重要的引理，就是对于每一轮的find的递归st[j]的值如果为false就表示这一轮的j的匹配不能改变了，这是因为如果中间存在st[j] = true的情况，可以分三种情况考虑1.match[j] == 0：此时表示整个匹配过程中j没被匹配，那么find返回的结果一定是true，也就表示最外层返回的结果一定是true，因为只要一层递归返回true，它的其他父层都一定能调整，所以一定可以回到第一层，最后第一层也能调整，表示第一轮匹配完成，进入下一轮，st会重置，。2.match[j] != 0 但是find(match[j]) =true，同样表示可以调整，根据上一种情况，也第一层也一定可以调整，所以这一轮的匹配也就已经结束了，所以j对应得对象在这一轮也不可能被改变了。3.match[j] != 0 但是find(match[j]) =false：这表明j虽然是在这一轮第一次出现，但是j在前几轮已经被匹配了，而且这次一想要调整她的对象还失败了，说明要么她的对象已经无法调整，要么他的对象可以调整，但是调整对象导致的别的女生需要被调整，而这些在这一轮的前几次for遍历中已经试过了（这些女生的st变为了false），结果这些女生无法被调整（不然就不会for到j了），所以无论哪种情况，都表示j匹配的对象在这一轮不能调整改变。所以总的来说，如果遍历了所有轮而最终的匹配数为k的话，那么由于每一轮男生匹配的女生在当前轮都没法调整了，而我又遍历了所有轮，所以一旦强行改变，那么最多就是匹配数+1 -1 不变（强行拆散一对导致-1，强行匹配一对导致+1），所以总匹配数<= k ；所以这种方案就是最大的匹配数了
rmk：本人也是一刷匈牙利，也没看什么相关的参考文献，纯粹是自己想了想做出的证明（应该叫说明•᷄ࡇ•᷅ ，以后有机会去看看算法导论，因为我是证明教信徒(^▽^)），所以可能算法证明的不是很严谨，甚至很可能出现一些问题，欢迎大佬指正
很好的例子！！如果不加memset(st,false,sizeof(st))的话结果会输出-1，因为在find(1)的时候st[1]被标记为了true，然后轮到find(2)的时候首先if(!st[j])这里的j==1，因为全局被标记了所以直接判断就不成立了。
ps：至于为什么样例要先输1 2再输1 1是因为链式向前星访问是以最后加的边开始的这样才会从1—1这条边开始
个人见解：输入加边的时候，编号是有可能重复的（因为左右部分的集合是分开编号的），为什么没有影响呢？（为什么还可以像之前那样处理呢？为什么不需要 add(b,a) 呢？）
因为题目的大前提就是这个图是二分图，加的边一定是 左集合的 u 与右集合的 v 相连，不会出现比如左集合中的两点连线这种情况。因此 add 方法的含义就不再是，增加图中两点之间的边了，而是增加两子图之间的边。具体而言，对于 add(a,b) 方法，含义为：加入一条 左集合编号为 a 与右集合编号为 b 的连线。按照这个定义，加入一条左集合编号为 u 到 右集合编号为 v 的边（即题目中输入边的定义），那就执行add(u,v)；如果你再执行 add(v,u)，意义就变成了 加入一条 左集合编号为 v 的点与右集合编号为 u 的点的连线，显然是错的。
预定的女孩A若有男朋友而且她原来的男朋友能够预定其它喜欢的女孩，是对原来男朋友为起点进行一次深搜，直到搜到一个没有男朋友的女孩B为止，这个女孩A换了男友是某个男生找到女孩B的效果
大佬图挂了
图论一刷 自己在csdn上写了一下二分图查找最大匹配的博文
如果st数组看不懂或者啥的可以去看看，交流交流也行
https://blog.csdn.net/WJPnb1/article/details/126332263
哪都有你
hh😄
这才是$acwing$的题解！
关于为什么预定之后如果没成功选择也不会取消预定，即
事实上，如果加上这行代码，小数据能过，大数据会TLE。这行代码加上去更好理解，但是降低了效率，不加这行也是正确的，下面给出分析：
按理来说，确实应该如果没成功匹配就取消预定，似乎不取消就白白占坑（女生）了
但其实可以这么想：如果A男生先预定B女生但是没能成功匹配，又去预定C女生结果和C女生成功匹配了，那么也不需要取消A男生对B女生的预定，因为如果A没能和B成功匹配，其他后来的男生更不能成功匹配。因为未分配的女生只会越来越少（比如C此时已经被预定掉了且match没有改变，A还能找C,B连C的机会都不可能有），后来男生只会比A更难。
说的生动一点就是，如果自己去找B女生都没成功，那么给占有其他男生现有的女生导致其他男生找B女生，那更是不能找到的
为啥每次循环都要初始化st数组
重置st是因为假设被A考虑过的女生如果也是B的心仪对象，在之后同样也可以被B考虑。
请问下这里的无向图存两条边为什么会错误？
因为全存的是左到右的路，你存第二条边存的也是左到右的路(不该存在)。
为什么要
if(!st[u]这个条件？不是每轮都会memset(st,false,sizeof st)，这样st都是false就一定成立了if(!st[u]）是为了保证匹配冲突时，换人匹配不去匹配已经匹配成功的点
讲得太好啦
可以用网络瘤证明
匹配原则：真心专一的人优先级大于广撒网的人；
为什么这题用邻接表，n=500，m = 100000不是稠密图吗，之前Dijkstra求最短路 I 一样的数据就是用邻接矩阵
我感觉可能是因为这里要的是对应 并没有涉及边的权重
tql
人人都笑黄毛，人人都是黄毛
我愿称之为牛头人算法
对于不同n1组节点，每轮find前不都重置了st[]数组的状态，这样在find()中，遍历连接的n2节点最初态都是false的，所以不太明白为什么还要判断 if( ! st[ j ] )，总感觉每次都是符合条件的，但不判断，又会出现超出内存错误。这是为什么呢？还是说我理解错了？
因为要递归调用find的时候不能再去找j啦
大佬 想问下这里的st数组 被预定怎么理解啊 这个预定是指的是被其他男生预定还是当前的男生呢 如果是当前男生的话 这里判断st[j]是不是false的意义在哪里呀 没大理解 希望有大佬指点一下
我感觉应该是当前这个男生，判断st是因为可能这个女生之前就已经和其他男生结成一对了，要想办法让他们分开
是的 差不多明白了 我现在的理解是这里判断女生是不是被预定是自己的女朋友被别人抢了以后(狗头)，再寻找其他喜欢的女生匹配时用到的，如果没有st这个判断并更新，就会使得这个男生一直循环自己喜欢的第一个女生了，就会出现死循环。
是的是的 这样解释就比较通俗了