最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定 $n$ 种面值的货币，每种货币可以选无数个

问：组成面值为 $m$ 的货币共有多少种方案

分析

这是一道 完全背包求方案数 的裸题，分析思路与上一题 AcWing 1023. 买书 完全一致

我就直接把上一题的题解贴过来了 不是在凑题解数，是真的一模一样没必要写

一共有 $n$ 个物品，每个物品有体积 $v_i$，价值 $w_i$，每个物品能够选多次

求总体积恰好为 $m$ 的 方案数

闫氏DP分析法

初始状态：f[0][0]

目标状态：f[n][m]

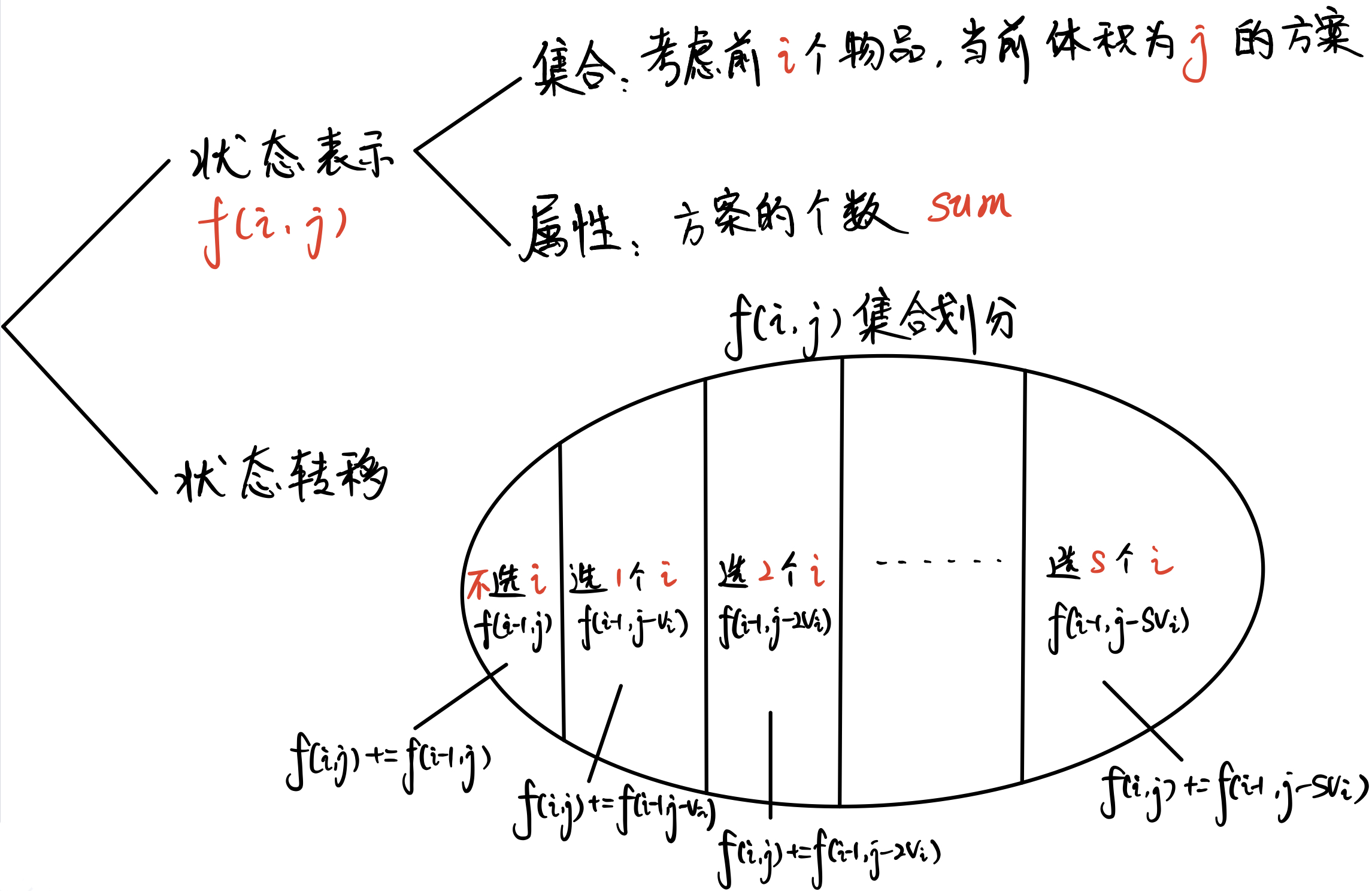
注意本题方案数会爆 int ，需要开 long long 来存状态

关于 空间/时间优化 ，可以参考这篇 AcWing 1023. 买书【完全背包求解方案数+空间/时间优化】

Code

时间复杂度：$O(n\times m)$

空间复杂度：$O(m)$

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 20, M = 3010;

int n, m;
int v[N];
LL f[M];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i];
    f[0] = 1;
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = v[i]; j <= m; ++ j)
        {
            f[j] += f[j - v[i]];
        }
    }
    cout << f[m] << endl;
    return 0;
}