最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定 $n$ 个正整数：$a_1, a_2, \cdots, a_n$

从中选出若干个数，使得他们的和为 $m$

求最终的 方案数

分析

对于本题我们可以把每个 正整数 看作是一个 物品

正整数 的值就是 物品 的 体积

我们方案选择的 目标 是最终 体积 恰好为 $m$ 时的 方案数

于是本题就变成了 01背包求解方案数 的问题了

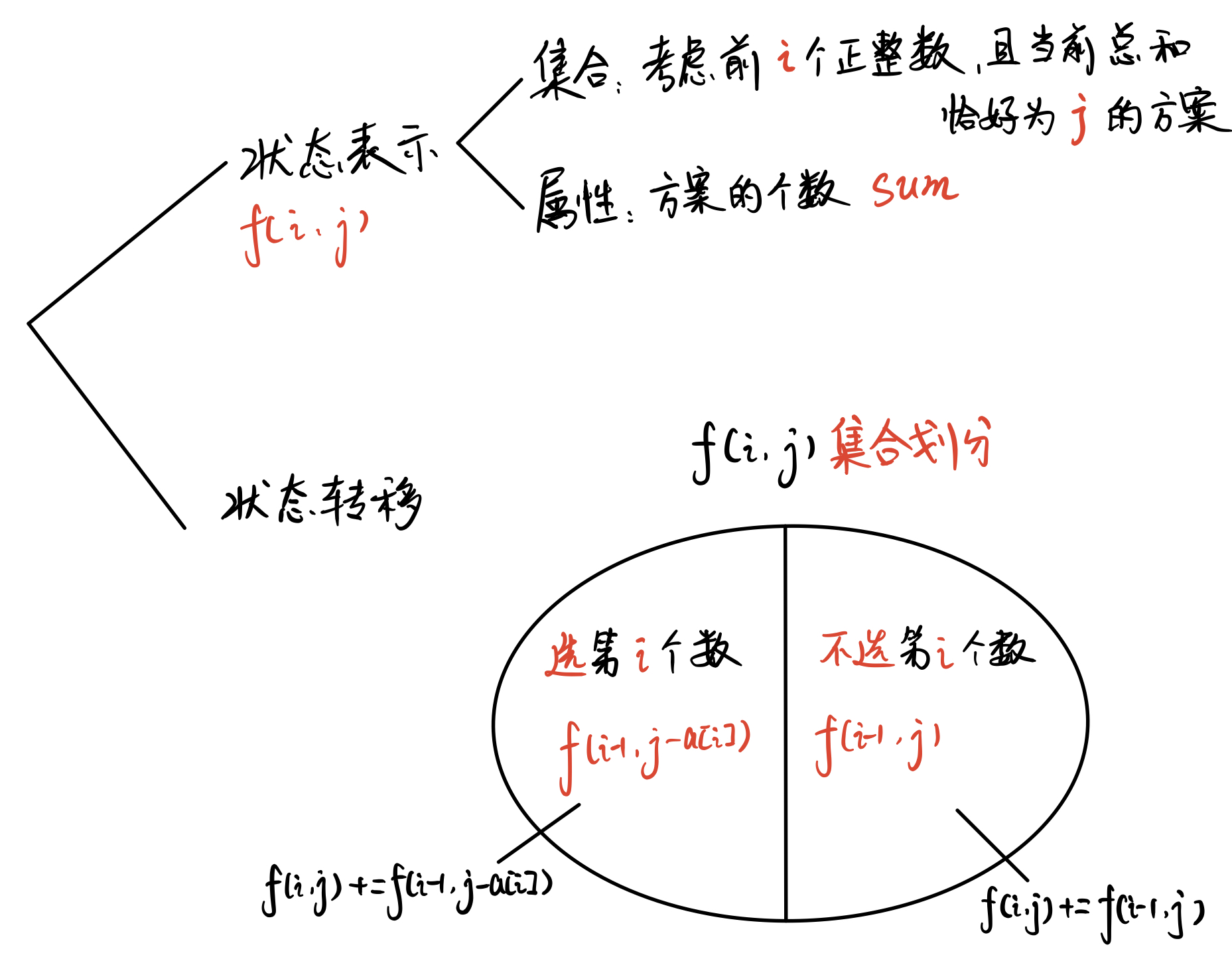
闫氏DP分析法

初始状态：f[0][0]

目标状态：f[n][m]

关于 01背包 的详细介绍和各种优化，可以看这篇博客 AcWing 423. 采药【01背包DP模型】

Code

时间复杂度：$O(n \times m)$

#include <iostream>

using namespace std;

const int N = 110, M = 10010;

int n, m;
int v[N];
int f[M];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i];

    f[0] = 1;
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = m; j >= v[i]; -- j)
        {
            f[j] += f[j - v[i]];
        }
    }
    cout << f[m] << endl;
    return 0;
}