最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

傻东西 和 皮神 一起去抓 宝可梦

一共会遇到 $n$ 个 野生宝可梦，小智有 $m$ 个 精灵球，皮神有 $t$ 滴 血

对于每个 野生宝可梦 来说，如果要捕捉他，需要 $v_{1i}$ 个 精灵球，战斗后皮神要掉 $v_{2i}$ 滴 血

如果皮神 血量 $\le 0$，则小智停止狩猎

小智对于每个 野生宝可梦 要么收服，要么逃跑

求一种方案：收服 尽可能多 的 野生宝可梦 ；如果收服数量一样，要皮神 血量最多

输出该方案的 野生宝可梦 收服数量，以及皮神战斗结束后的 剩余血量

分析

y总在标签里很贴心的贴了一个 阅读理解 的tag，没错这就是一道阅读理解题

本题是一道 01背包 的扩展题 —— 二维费用01背包问题

把 野生宝可梦 看做物品，则捕捉他需要的 精灵球 个数就是第一费用，战斗皮神要掉的血就是第二费用

最后答案要求物品数量最多，因此我们可以用状态的属性来表示选择的物品数

以上就是本题的 阅读理解分析部分 ，接下来直接上闫氏DP分析法

闫氏DP分析法

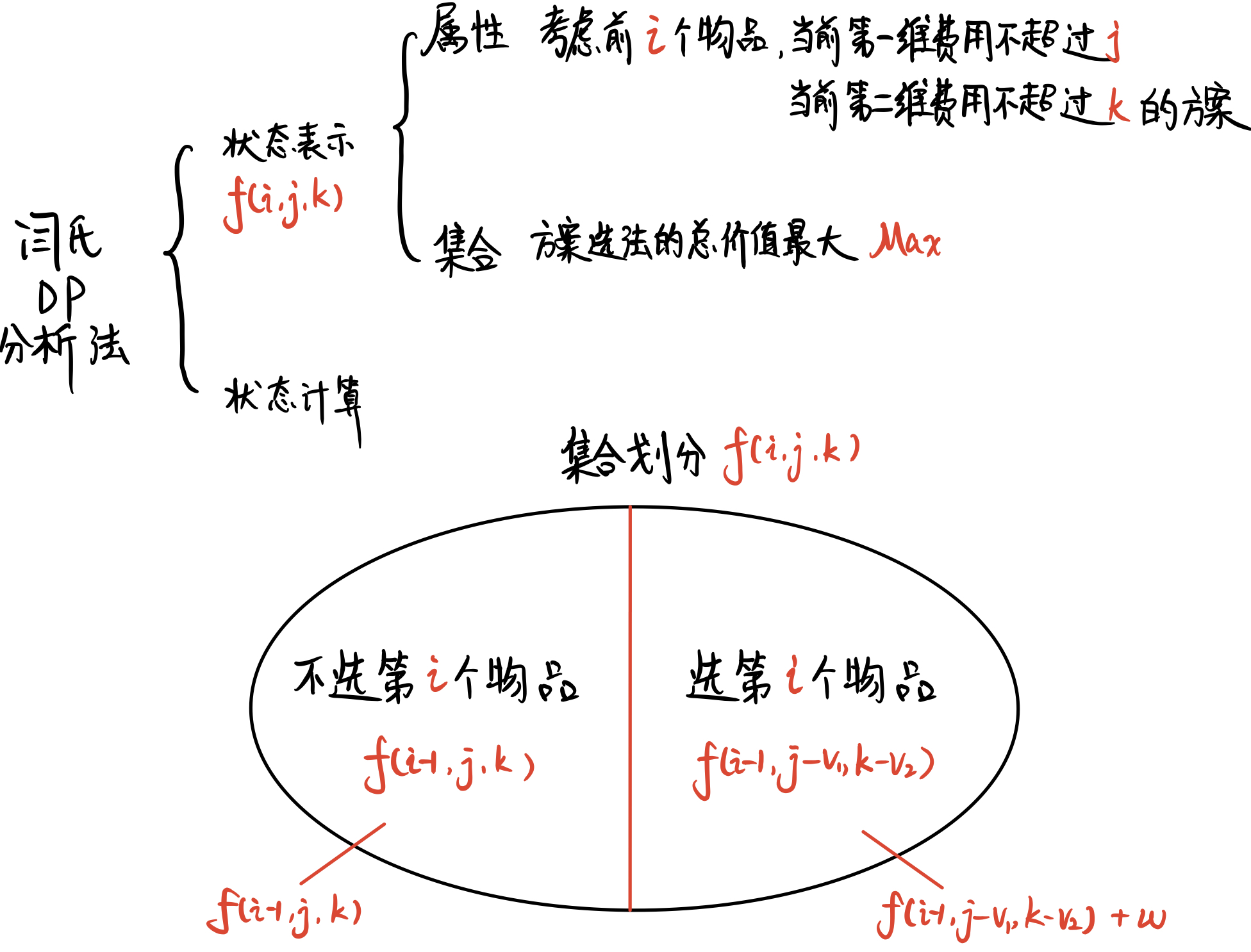
初始状态：f[0][0][0]
目标状态：f[n][m][t - 1] （皮神不能 再起不能 才算抓住那个 宝可梦 ）

Code

时间复杂度：$O(n \times m \times k)$

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 110, M = 1010, K = 510;

int n, m, t;
int v1[N], v2[N];
int f[M][K];

int main()
{
    //input
    cin >> m >> t >> n;
    for (int i = 1; i <= n; ++ i) cin >> v1[i] >> v2[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = m; j >= v1[i]; -- j)
        {
            for (int k = t - 1; k >= v2[i]; -- k)
            {
                f[j][k] = max(f[j][k], f[j - v1[i]][k - v2[i]] + 1);
            }
        }
    }

    //output
    cout << f[m][t - 1] << " ";
    //找到满足最大价值的所有状态里，第二维费用消耗最少的
    int cost_health = t;
    for (int k = 0; k <= t - 1; ++ k)
    {
        if (f[m][k] == f[m][t - 1])
        {
            cost_health = min(cost_health, k);
        }
    }
    cout << t - cost_health << endl;
    return 0;
}