最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

我在野区采灵芝

题目描述

题目给定 $n$ 株草药 和 $m$ 个单位时间

接着给定每株草药如果被采集，所需要的的时间 $v$，以及该草药的价值 $w$

让我们求出一种采药 方案 ，在给定的时间 $m$ 内，能够采集到的草药的 最大价值

分析

我们把 $m$ 个单位时间看做是 背包的容量

每株草药看做是 物品 ，草药采集所需时间看做是 物品的体积，草药的价值看做是 物品的价值

那么本题就可以看做是一个 背包问题 了

由于每株草药只有一个，也就是要么采，要么不采两种方案，所以该题是一个 01背包 模型

01背包模型

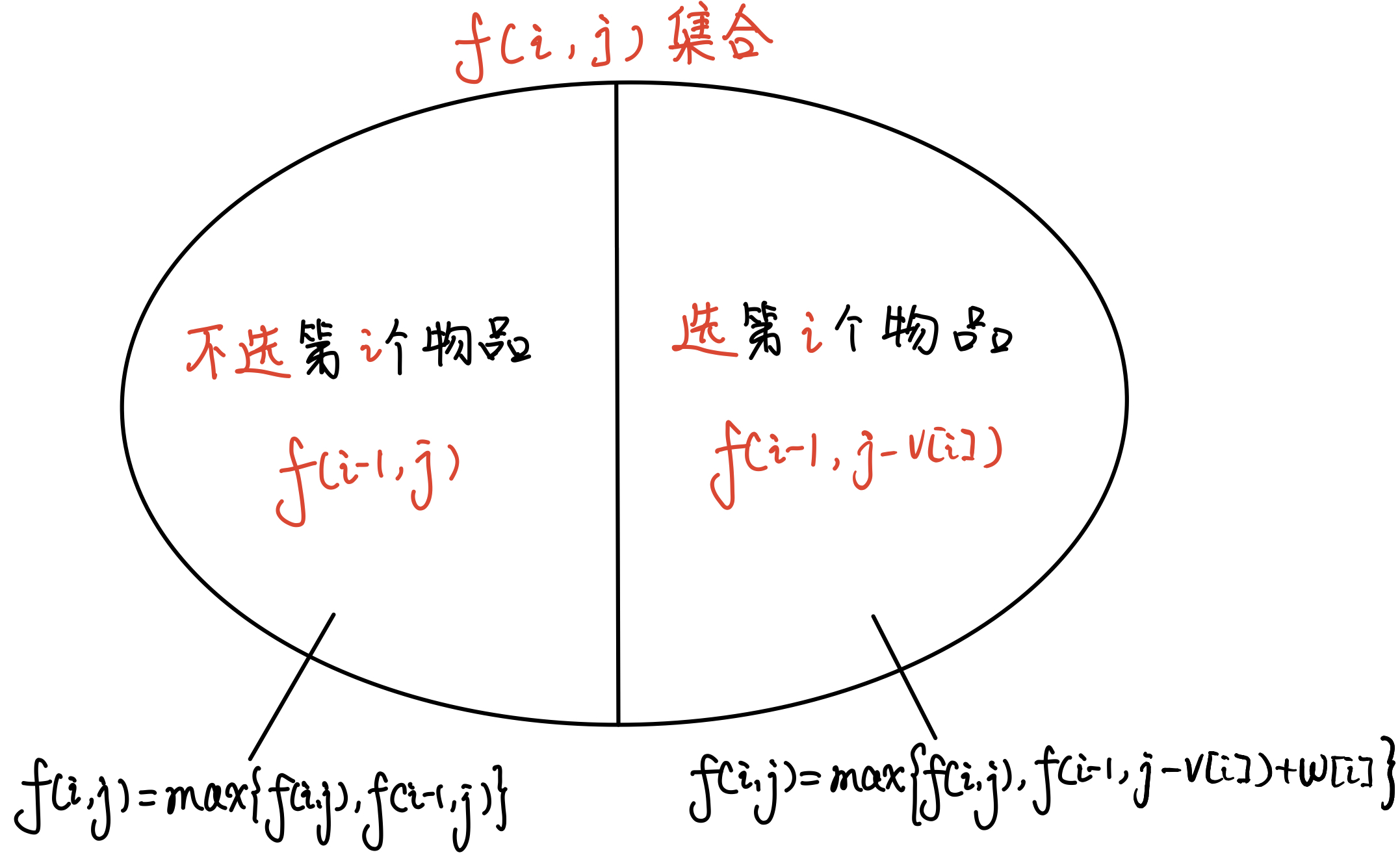
状态表示$f(i,j)$—集合： 考虑前 i 个物品，且当前已使用体积不超过 j 的方案

状态表示$f(i,j)$—属性： 该方案的价值为最大值 $\max$

状态转移$f(i,j)$： $f(i,j) = \begin{cases} 不选第i个物品： &\max\{f(i-1,j)\} \\\ 选第i个物品：&\max\{f(i-1,j - v_i) + w_i\} \end{cases}$

初始状态：f[0][0]
目标状态：f[n][m]

集合划分

Code(朴素版)

空间复杂度：$O(n \times m)$
时间复杂度：$O(n \times m)$

#include <iostream>

using namespace std;

const int N = 110, M = 1010;

int n, m;
int w[N], v[N];
int f[N][M];

int main()
{
    //input
    cin >> m >> n;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= m; ++ j)
        {
            f[i][j] = f[i - 1][j];//不选
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);//选
        }
    }

    //output
    cout << f[n][m] << endl;
    return 0;
}

Code(空间优化)

空间复杂度：$O(m)$
时间复杂度：$O(n \times m)$

观察到朴素版的代码里，每个阶段 i 的状态转移，只依靠 i-1 层的状态

因此我们可以通过 滚动数组 或者 代码等价变形 来优化掉后续不再使用的空间

滚动数组

#include <iostream>

using namespace std;

const int N = 110, M = 1010;

int n, m;
int w[N], v[N];
int f[2][M];

int main()
{
    //input
    cin >> m >> n;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= m; ++ j)
        {
            f[i & 1][j] = f[i - 1 & 1][j];//不选
            if (j >= v[i]) f[i & 1][j] = max(f[i & 1][j], f[i - 1 & 1][j - v[i]] + w[i]);//选
        }
    }

    //output
    cout << f[n & 1][m] << endl;
    return 0;
}

代码等价变形（经典01背包优化方式）

#include <iostream>

using namespace std;

const int N = 110, M = 1010;

int n, m;
int w[N], v[N];
int f[M];

int main()
{
    //input
    cin >> m >> n;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = m; j >= v[i]; -- j)
        {
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }

    //output
    cout << f[m] << endl;
    return 0;
}