算法
(动态规划) $O(n^2m)$
我们先来回顾一下闫氏DP分析法的基本思想：
所有DP问题都可以从集合角度来解释。一般的DP问题都是在有限集合内求最值或求个数，极个别的DP问题会在无限集合内求最值，此时先将无限集想办法缩小到有限集即可，例如AcWing 273. 分级。
然后我们考虑如何从本题的所有饼干分配方案的集合中，找出最小值。
此题的整体思想和AcWing 734. 能量石类似，都是先用贪心将最优解缩小到某个较小的范围内，再DP求出精确的最优解。
根据排序不等式，我们发现在本问题所包括的分配方案的全集中，最优解一定在如下的子集中：
- 将所有小朋友按愤怒值g[i]从大小到小排序，排名靠前的小朋友分配的饼干要更多一些。
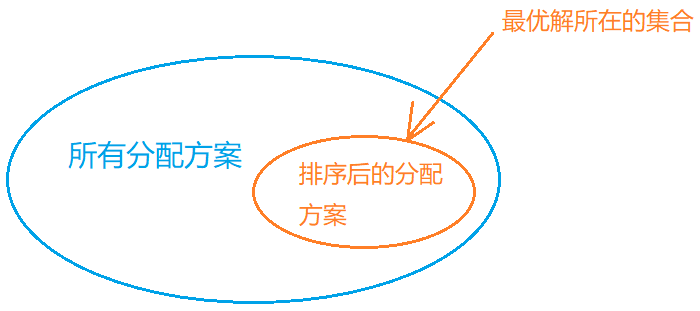
接下来我们只需在橘黄色框出的子集中用DP寻找最优解即可。
首先将所有小朋友按g[i]从大到小排序。
此题的状态划分方式与AcWing 900. 整数划分类似，前者是以最小数是不是1来划分，后者是以最后有几个1来划分的。分析图如下所示：
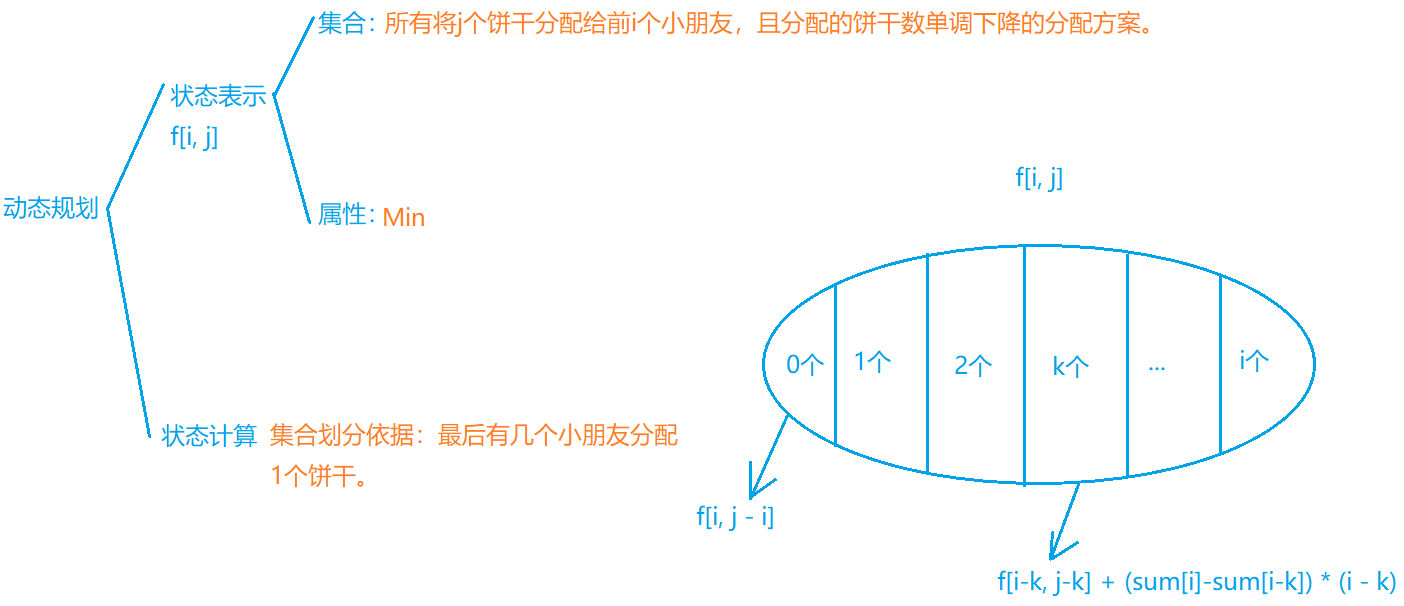
最后求方案数只需倒推一遍，找出每个状态是由哪个状态计算得到的即可。
时间复杂度
一共有 $n * m$ 个状态，计算每个状态需要 $O(n)$ 的计算量，因此总时间复杂度是 $O(n^2m)$。
参考文献
- 《算法竞赛进阶指南》
C++ 代码
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 31, M = 5010;
int n, m;
PII g[N];
int s[N];
int f[N][M];
int ans[N];
int main()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++ )
{
cin >> g[i].first;
g[i].second = i;
}
sort(g + 1, g + n + 1);
reverse(g + 1, g + n + 1);
for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + g[i].first;
memset(f, 0x3f, sizeof f);
f[0][0] = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
if (j >= i) f[i][j] = f[i][j - i];
for (int k = 1; k <= i && k <= j; k ++ )
f[i][j] = min(f[i][j], f[i - k][j - k] + (s[i] - s[i - k]) * (i - k));
}
cout << f[n][m] << endl;
int i = n, j = m, h = 0;
while (i && j)
{
if (j >= i && f[i][j] == f[i][j - i]) j -= i, h ++ ;
else
{
for (int k = 1; k <= i && k <= j; k ++ )
if (f[i][j] == f[i - k][j - k] + (s[i] - s[i - k]) * (i - k))
{
for (int u = i; u > i - k; u -- )
ans[g[u].second] = 1 + h;
i -= k, j -= k;
break;
}
}
}
for (int i = 1; i <= n; i ++ ) cout << ans[i] << ' ';
cout << endl;
return 0;
}
能再详细说一下如何倒推吗，完全不懂
yls，因为每个孩子至少要分一个饼干，所以状态转移的时候j可以从i开始，同理，由答案反推方案时就保证了反推过程中 i <= j，可以减少不必要的判断。
“从大小到小排序”(这是不是多了一个小
y总能找些和这题类似的题目吗
Y老师 为什么 h++后， 没有对ans数组的前i个 +1， 却能得到正确的方案数啊。
我知道h 表示前i个数整体上升的值， 但最后却加到 后面全是1的数上，有点难以理解。（按照定义，h 应该是前i个小朋友饼干数+1吧？） 为什么会是后面k个小朋友 +h 呢
这里对后面k个小朋友+h了并不意味着对前面的小朋友什么也没做，因为这里加了之后h并没有清零，所以待会儿就会给前面的小朋友加这个h的。
h表示前面的小朋友整体需要加的数，所以让h加1，就是让前面的所有小朋友都加1了。
请问下j >= i，为什么能够保证第i个小朋友分得饼干数目大于1呢？很可能第i个小朋友分得的饼干数目就是1
不一定大于1啊，这里会枚举到所有子集，当
k >= 1时第i个小朋友分到饼干数量就是1。建议看一下视频讲解AcWing 277. 饼干（《算法竞赛进阶指南》打卡活动）。y总，第二种情况下也满足j>=i，那么，它也会f[i][j]=f[i][j-i],那它最小的饼干数不就会变成0了吗
图里的0不是最小饼干数，是指有0个小朋友的饼干数是1。
枚举k个1的时候，前i-k个数一定都比1大吗？ f[i-k][j-k]这个集合的最优解可能是最后几个都是1，这种情况怎么办呢？
注意看划分的定义，前
i - k个数一定比1大。f[i - k, j - k]用了映射思想，是说这种集合里的方案数量和f[i - k, j - k]所表示的集合中的方案数量相同。具体可以参考本题的讲解视频：AcWing 277. 饼干（《算法竞赛进阶指南》打卡活动）。前$i-k$个数一定都比1大这是如何保证的呢？ $f[i - k, j - k]$表示的是将前$j-k$个饼干分给前$i-k$个小朋友的最小代价，无法保证$f[i - k, j - k]$的这个最优的集合一定不包含1
我举个例子吧：比如说 $ f[2][3] $ 的最优解一定是 第一个小朋友分配2块饼干，第二个小朋友分配1块饼干 ， 当我们求解$f[3][4]$ 的时候我们枚举第三个小朋友分了1块饼干，而且我们认为前两个小朋友分到的饼干一定比第三个小朋友多，此时有 $f[3][4] = f[2][3] + 2*(s[3] -s[2])$. 那这个时候显然就是不对的了，因为第二个小朋友分配的饼干数也是1个，所以此时只有一个小朋友比第三个小朋友分配的饼干要多。
这种情况会在枚举
k = 2的时候取到最优解。这里是映射的思想，因为本题的目标值只跟小朋友的饼干数量的相对大小有关，和绝对数量无关，枚举 $k$ 的时候，前 $i - k$ 个小朋友的每一种分配方案，和
f[i - k, j - k]的分配方案是一一对应的，但并没有说这两种方案一模一样，要先明确“映射”的含义。所以建议先完整看一遍上面评论里给出的视频，视频里这里讲得很清楚的。这是闫氏DP分析法的精髓hh
讲的好清楚，看蓝书蒙蔽半天，看这个图瞬间就懂了
大部分DP问题都可以从集合角度来分析，会清楚很多。
大佬好拼命阿！
今天下午就要讲了，必须要先备好课啊。