题目描述
几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第 k 小的数字吗?
乘法表是大小为 m x n 的一个整数矩阵,其中 mat[i][j] == i * j(下标从 1 开始)。
给你三个整数 m、n 和 k,请你在大小为 m x n 的乘法表中,找出并返回第 k 小的数字。
样例
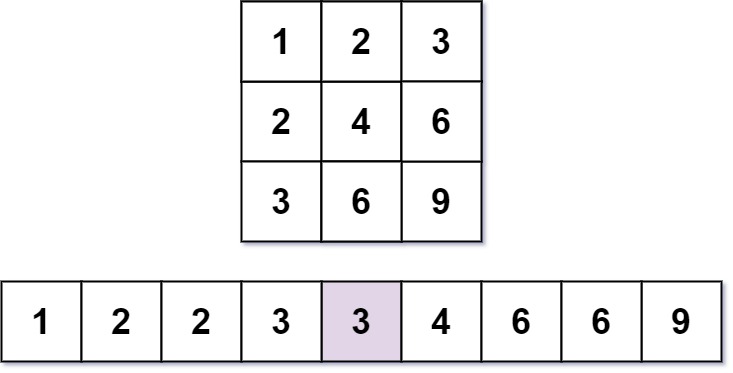
输入:m = 3, n = 3, k = 5
输出:3
解释:第 5 小的数字是 3。
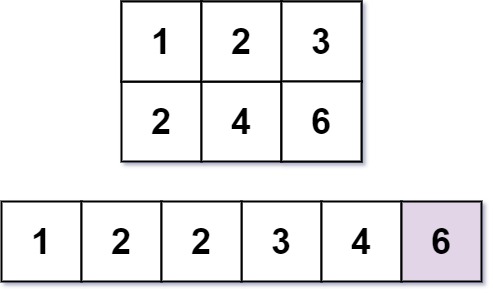
输入:m = 2, n = 3, k = 6
输出:6
解释:第 6 小的数字是 6。
限制
1 <= m, n <= 3 * 10^41 <= k <= m * n
算法
(二分答案) O(m∗log(m∗n))
- 很容易发现,给定一个数字
x,我们可以计算出x在乘法表中排多少。而且我们找数字的过程是单调的,故可以使用二分的方法来查找第k小的数字。 - 判定
x的过程可以枚举每一行,用x / i可以计算出这一行中有多少小于等于x的数字。
时间复杂度
- 判定的时间复杂度为 O(m),二分的时间复杂度为 O(log(m∗n)),故总时间复杂度为 O(m∗log(m∗n))。
C++ 代码
class Solution {
public:
int check(int x, int m, int n) {
int tot = 0;
for (int i = 1; i <= m; i++)
tot += min(n, x / i);
return tot;
}
int findKthNumber(int m, int n, int k) {
int l = 1, r = n * m;
while (l < r) {
int mid = (l + r) >> 1;
if (k <= check(mid, m, n))
r = mid;
else
l = mid + 1;
}
return l;
}
};


看老哥的题解长大的
为啥不能k >= check(mid, m, n)这样呢
因为二分划分的两段是 [l,mid] 以及 [mid+1,r],如果用 >= 需要检查 mid + 1
佬我这样理解可以吗?因为我们计算check(mid, m, n)的时候是找到乘法表中最后一个出现的数,例如3*3的表中 比2小的是3个但是它是答案,([1,2,2,3,3,4,6,6,9])按照二分的思想它应该也是为true的!因此可以推断出答案是在右区间上的
可以,二分边界问题其实不复杂,在离散域(整数)的情况下,定义好两个划分的区间段后,例如 [l,mid] 和 [mid+1,r],则有几种判定方式,一种是判定目标小于等于 mid 在左区间,另一种就是判定目标大于等于 mid+1 在右区间。也可以判定目标大于 mid 在右区间,或者目标小于 mid+1 在左区间。这几种方式可能对应不同的 check 逻辑,根据实际情况选择最合适的判断方式。
alternative implementation
template <class F> struct recursive { F f; template <class... Ts> decltype(auto) operator()(Ts&&... ts) const { return f(std::ref(*this), std::forward<Ts>(ts)...); } template <class... Ts> decltype(auto) operator()(Ts&&... ts) { return f(std::ref(*this), std::forward<Ts>(ts)...); } }; template <class F> recursive(F) -> recursive<F>; auto const rec = [](auto f){ return recursive{std::move(f)}; }; class Solution { public: int findKthNumber(int m, int n, int k) { auto binary_search = [&](auto ll, auto rr, auto target, auto &&f) { optional<decltype(ll)> answer = std::nullopt; auto search = rec([&](auto&& search, auto ll, auto rr) -> void { auto mid = ll + (rr - ll) / 2; if (ll > rr) return; else if (f(mid) >= target) (answer = mid, search(ll, mid - 1)); else if (f(mid) < target) search(mid + 1, rr); }); return (search(ll, rr), answer); }; auto rank = [&](int x, int acc = 0) { for (int i = 1; i <= m; i++) acc += min(n, x / i); return acc; }; return *binary_search(1, m * n, k, rank); } };