思路要点

• 本题属于最优解问题，可采用集合的思想，分类讨论进行求解。分类的标准是“可重、不漏”。（对于求数量的问题，分类的标准是“不重不漏”）
• 对于这道题目而言，分类标准可以是：环上最大节点编号分别为$1, 2, …, n$，则对于这每一种情况，通过枚举所有可能的环而找出最优解，如下图所示。
  
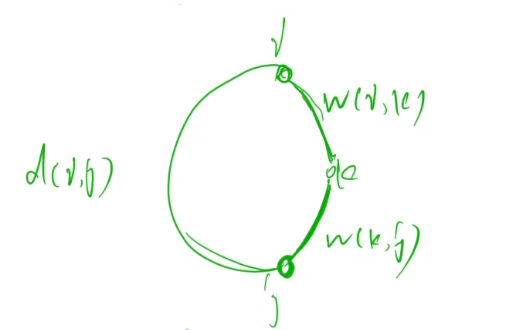
  在上图中，假设环的最大节点编号是k，则可对小于k的节点进行枚举，即i和j。由于k与i之间的距离、k与j之间的距离是确定的，要想环的长度之和最小，i与j之间的距离就应该取最短路，且最短路所包含的点编号都必须小于k（假设的限制）。
• 在floyd算法中，第一层循环具有的含义是：在执行第k层循环之前，d数组中存储的就是编号为1,...,k-1的节点之间的最短路的长度。
• 关于如何记录下来最短路的路径（由于对floyd算法原理了解的并不深，下面是目前的理解，求路径的写法至少要背下来）
  当d[i][k] + d[k][j] < d[i][j]时，d[i][j]会发生更新，则当前的最短路里面就应包含中间节点k，可类似本题中用pos数组存储下来，然后通过递归来推导出完整路径。

代码

import java.util.*;

public class Main
{
    static int N = 110, INF = 0x3f3f3f3f;
    static int n, m;
    static int[][] g = new int[N][N];
    static int[][] d = new int[N][N];
    static int[][] pos = new int[N][N];
    static int[] path = new int[N];
    static int cnt;
    static int res = INF;

    public static void solve()
    {
        // floyd算法的第一层循环
        // 这里第k层循环(即已执行完k-1层循环时)表示的含义是：对于编号是1,...,k-1这些节点，d数组所存储的值是它们之间的最短路的长度
        for(int k = 1; k <= n; k ++) 
        {
            // 对于环上节点编号的最大值是k的情况，通过枚举相邻节点，找出最小环长度和方案
            for(int i = 1; i < k; i ++)
                for(int j = i + 1; j < k; j ++)
                {
                    if((long)g[k][i] + d[i][j] + g[j][k] < res)
                    {
                        res = g[k][i] + d[i][j] + g[j][k];
                        cnt = 0;
                        path[cnt ++] = k;
                        path[cnt ++] = i;
                        getPath(i, j);
                        path[cnt ++] = j;
                    }
                }


            // floyd算法的后两层循环
            // pos数组用于记录最短路的路径，可递归求解出
            for(int i = 1; i <= n; i ++)
                for(int j = 1; j <= n; j ++)
                    if(d[i][k] + d[k][j] < d[i][j])
                    {
                        d[i][j] = d[i][k] + d[k][j];
                        pos[i][j] = k;
                    }
        }
    }

    // 递归求解节点x，y之间的最短路所经过的节点编号
    public static void getPath(int x, int y)
    {
        if(pos[x][y] == 0) return; // 节点x，y之间不包含中间节点，说明x,y相连通或x,y是相同的节点

        int m = pos[x][y];
        getPath(x, m);
        path[cnt ++] = m;
        getPath(m, y);
    }

    public static void main(String[] args)
    {
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        for(int i = 0; i < N; i ++)
            for(int j = 0; j < N; j ++)
                if(i == j) g[i][j] = 0;
                else g[i][j] = INF;
        for(int i = 0; i < m; i ++)
        {
            int a = sc.nextInt(), b = sc.nextInt();
            int l = sc.nextInt();
            g[a][b] = Math.min(g[a][b], l);
            g[b][a] = g[a][b];
        }
        for(int i = 0; i < N; i ++)
            for(int j = 0; j < N; j ++)
                d[i][j] = g[i][j];

        solve();
        if(res == INF) System.out.println("No solution.");
        else
        {
            for(int i = 0; i < cnt; i ++) System.out.print(path[i] + " ");
        }
    }
}