最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

给定两个长度为 $n$ 个数组 $a[n], b[n]$

求两个数组的 最长公共上升子序列 长度

解析

这是两个经典DP模型的结合版：

$\text{LIS}$ (最长上升子序列，Longest Increasing Subsequence)

$\text{LCS}$ (最长公共子序列，Longest Common Subsequence)

$\text{LCIS}$ (最长公共上升子序列，Longest Common Increasing Subsequence)

LCIS 也是一个相当经典的DP模型，他的 状态分析 是 LIS 与 LCS 的结合，且听我慢慢道来

闫氏DP分析法：(结合了LCS与LIS的状态表示的方法，可以很直接的发现二者的影子)

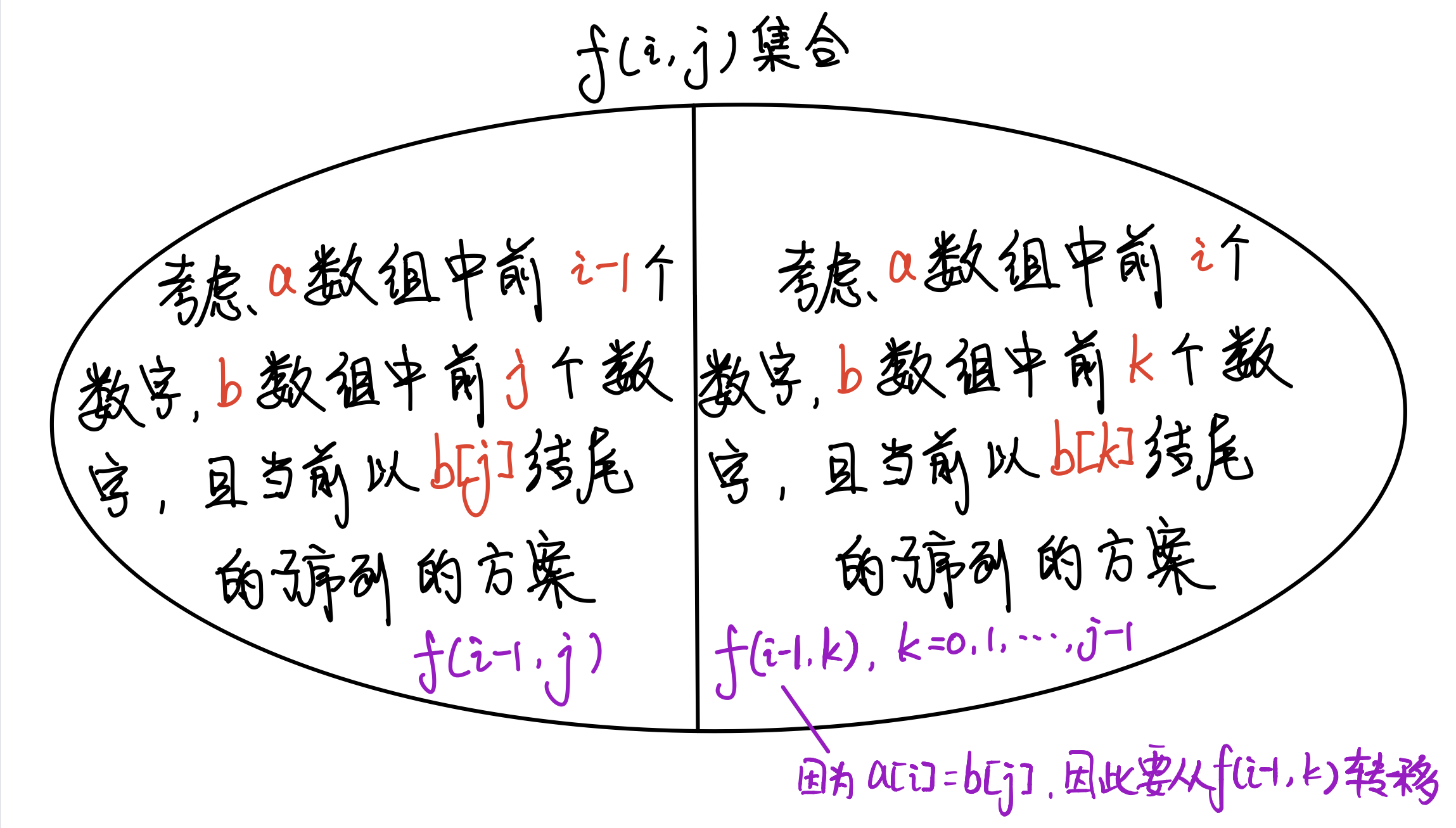
状态表示 f[i][j]—集合：考虑 a 中前 i 个数字，b 中前 j 个数字 ，且当前以 b[j] 结尾的子序列的方案

状态表示 f[i][j]—属性：该方案的子序列长度最大 $\max$

状态转移 ：

1. 从考虑 a数组 中前 i-1 个数字， b数组 中前 j 个数字 ，且当前以 b[j] 结尾的子序列的方案转移过来：
   $f_{i,j}=\max(f_{i,j}, f_{i-1,j})$

2. 从考虑 a数组 中前 i 个数字， b数组 中前 k 个数字 ，且当前以 b[k] 结尾的子序列的方案转移过来：
   $f_{i,j}=\max(f_{i,j}, f_{i-1,k} + 1) \quad k\in[0,j-1],a_i = b_j,b_j>b_k$

初始状态：f[0][0]

目标状态：f[n][i]

集合划分

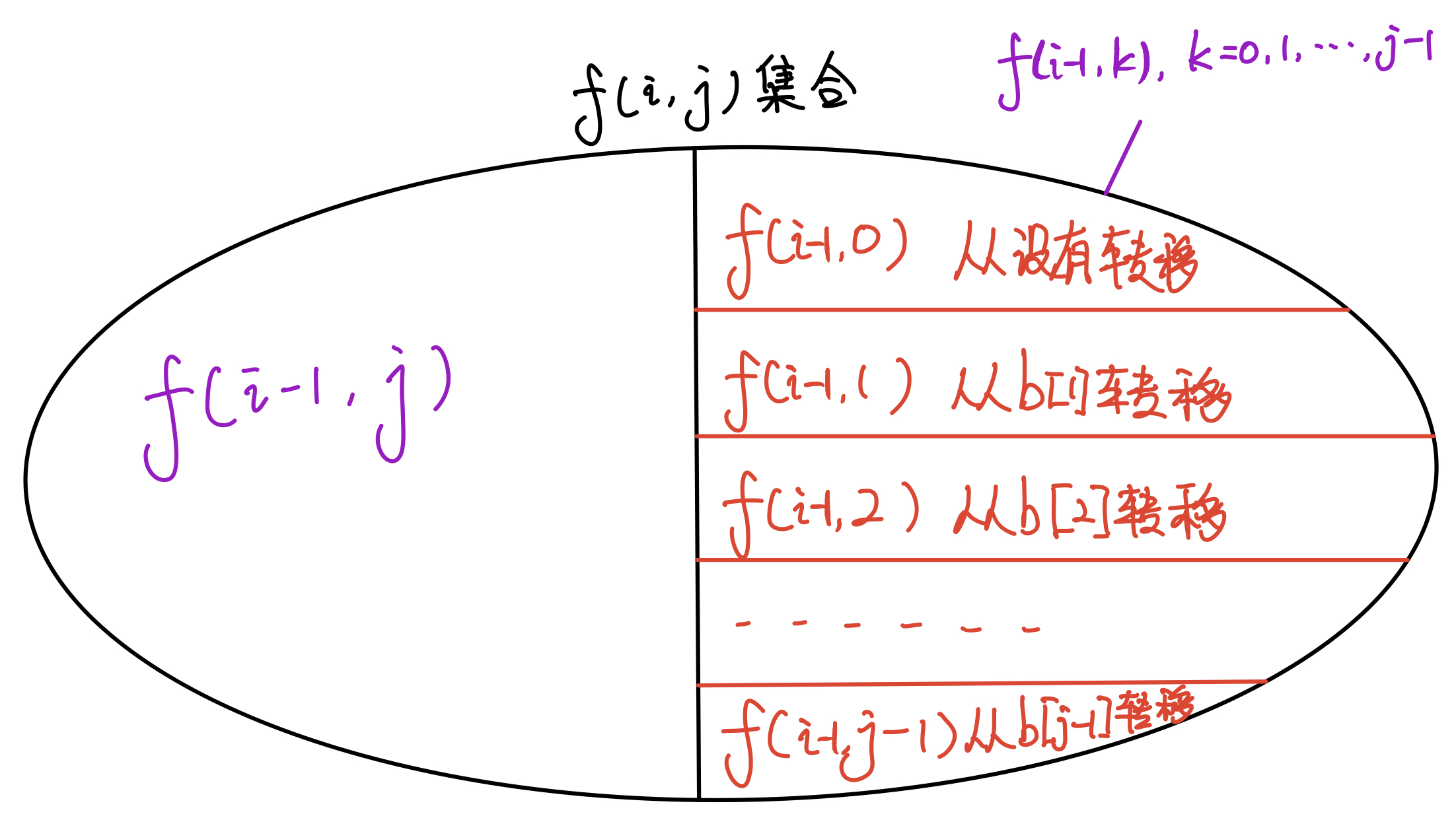
Code（朴素版）

时间复杂度：$O(n^3)$

对于本题的数据规模，毫无疑问会超时

这里贴出代码是方便大家理解这个DP模型，因为接下来的优化，就和DP无关，是一个代码的等价变形优化

#include <iostream>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    //input
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> a[i];
    for (int i = 1; i <= n; ++ i) cin >> b[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 1; j <= n; ++ j)
        {
            f[i][j] = f[i - 1][j];
            if (a[i] == b[j])
            {
                for (int k = 0; k < j; ++ k)
                {
                    if (b[j] > b[k])
                    {
                        f[i][j] = max(f[i][j], f[i - 1][k] + 1);
                    }
                }
            }
        }
    }

    //find result
    int res = 0;
    for (int i = 0; i <= n; ++ i) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}

Code（优化版）

我们可以观察到，对于第二种状态转移：$f_{i,j}=\max(f_{i,j}, f_{i-1,k} + 1) \quad k\in[0,j-1],a_i = b_j,b_j>b_k$

每次用到的 状态 都是第 i - 1 个阶段的

因此我们可以用一个变量，存储上一个阶段的能够接在 a[i] 前面的最大的状态值

时间复杂度：$O(n^2)$

#include <iostream>

using namespace std;

const int N = 3010;

int n;
int a[N], b[N];
int f[N][N];

int main()
{
    //input
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> a[i];
    for (int i = 1; i <= n; ++ i) cin >> b[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        int maxv = 1;
        for (int j = 1; j <= n; ++ j)
        {
            f[i][j] = f[i - 1][j];
            if (b[j] == a[i]) f[i][j] = max(f[i][j], maxv);
            if (b[j] < a[i]) maxv = max(maxv, f[i - 1][j] + 1);
        }
    }

    //find result
    int res = 0;
    for (int i = 0; i <= n; ++ i) res = max(res, f[n][i]);
    cout << res << endl;

    return 0;
}