题目描述

小扣参加的秋日市集景区共有 N 个景点，景点编号为 1 ~ N。景点内设有 N-1 条双向道路，使所有景点形成了一个二叉树结构，根结点记为 root，景点编号即为节点值。

由于秋日市集景区的结构特殊，游客很容易迷路，主办方决定在景区的若干个景点设置导航装置，按照所在景点编号升序排列后定义装置编号为 1 ~ M。导航装置向游客发送数据，数据内容为列表 [游客与装置 1 的相对距离,游客与装置 2 的相对距离,...,游客与装置 M 的相对距离]。由于游客根据导航装置发送的信息来确认位置，因此主办方需保证游客在每个景点接收的数据信息皆不相同。请返回主办方最少需要设置多少个导航装置。

样例

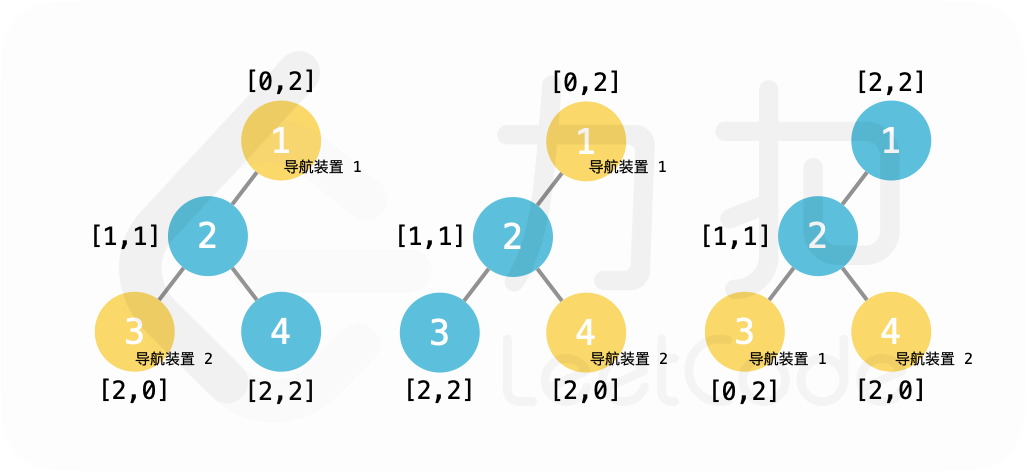
输入：root = [1,2,null,3,4]
输出：2
解释：在景点 1、3 或景点 1、4 或景点 3、4 设置导航装置。

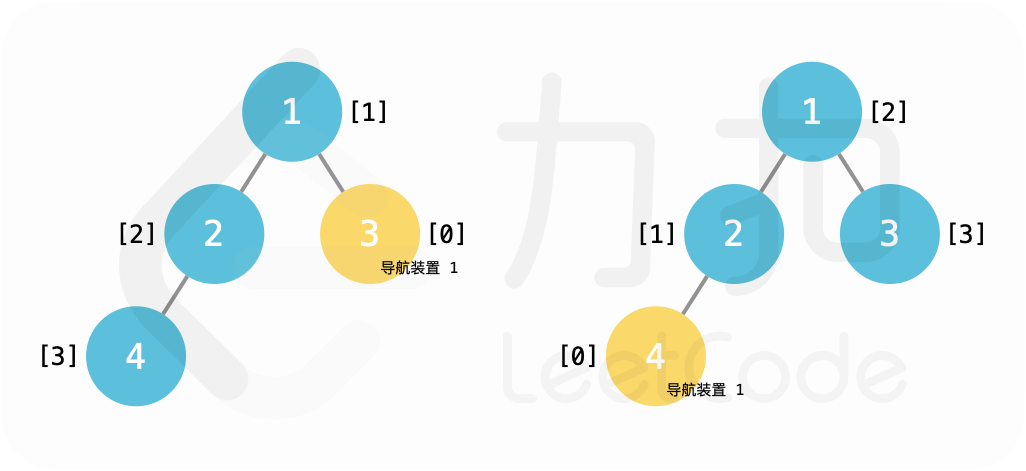
输入：root = [1,2,3,4]
输出：1
解释：在景点 3、4 设置导航装置皆可。

限制

• 2 <= N <= 50000
• 二叉树的非空节点值为 1 ~ N 的一个排列。

算法

(动态规划) $O(n)$

1. 观察发现，对于每一个三叉节点，都需要至少有两个分叉的子树存在导航装置。对于一个二叉节点，仅需要任意一个分叉含有导航装置。
2. 根据以上规则，通过动态规划自底向上递归求解。除根节点外，每个节点都含有父节点，所以通过定义三种状态来分类讨论。
3. 设状态 $f(u, 0)$ 表示以 $u$ 为根节点的子树，状态为已经含有装置，且通过父节点的分支无需再含有装置。$f(u, 1)$ 表示子树没有任何装置。$f(u, 2)$ 表示子树已经含有装置，但通过父节点的分支还需要拥有装置。
4. 对于非根节点：
   • 如果为叶子节点，则 $f(u, 0) = 1$，$f(u, 1) = 0$，$f(u, 2) = +\infty$。
   • 如果只有左子树或者右子树，则 $f(u, 0) = \min(f(son, 0), f(son, 1) + 1, f(son, 2) + 1)$；$f(u, 1) = f(son, 1)$；$f(u, 2) = f(son, 2)$。
   • 如果同时存在有左右子树，则此节点就是三叉节点：
     • 对于 $f(u, 0)$，则根据子树中是否含有装置进行转移。如果都没有装置，则需要补齐两个装置；如果只有一个装置，则需要再补齐一个装置。否则，两个子树互相都可以满足，无需额外的装置。
     • $f(u, 1) = +\infty$，即经过三叉节点后，不可能会出现没有装置的情况。
     • 对于 $f(u, 2)$，也是类似的讨论方式。如果都没有装置，则需要补齐一个装置。剩余情况可以自行通过代码分析判断。
5. 对于根节点，只有一个子树的情况，则直接返回 $\min(f(son, 0), f(son, 1) + 1, f(son, 2) + 1)$。对于两个子树的情况，此处需要特别注意，根节点不再是三叉节点，可以自行通过代码分析判断。

时间复杂度

• 每个节点仅遍历一次，故总时间复杂度为 $O(n)$。

空间复杂度

• 需要 $O(n)$ 的额外空间存储动态规划的状态。

C++ 代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

const int N = 50010;

class Solution {
private:
    int f[N][3];

    void solve(TreeNode *u) {
        if (!u) return;
        solve(u->left);
        solve(u->right);

        int l = 0, r = 0;
        if (u->left) l = u->left->val;
        if (u->right) r = u->right->val;

        int val = u->val;

        if (l == 0 && r == 0) {
            f[val][0] = 1;
            f[val][1] = 0;
            f[val][2] = N;
        } else if (l == 0) {
            f[val][0] = min(f[r][0], min(f[r][1], f[r][2]) + 1);
            f[val][1] = f[r][1];
            f[val][2] = f[r][2];
        } else if (r == 0) {
            f[val][0] = min(f[l][0], min(f[l][1], f[l][2]) + 1);
            f[val][1] = f[l][1];
            f[val][2] = f[l][2];
        } else {
            f[val][0] = N;
            for (int i = 0; i < 3; i++)
                for (int j = 0; j < 3; j++)
                    f[val][0] = min(f[val][0],
                        f[l][i] + f[r][j] + (i == 1) + (j == 1));

            f[val][1] = N;

            f[val][2] = N;
            f[val][2] = min(f[val][2], f[l][0] + f[r][1]);
            f[val][2] = min(f[val][2], f[l][1] + f[r][0]);
            f[val][2] = min(f[val][2], f[l][1] + f[r][1] + 1);
            f[val][2] = min(f[val][2], f[l][1] + f[r][2]);
            f[val][2] = min(f[val][2], f[l][2] + f[r][1]);
        }
    }

public:
    int navigation(TreeNode* root) {
        solve(root->left);
        solve(root->right);

        int l = 0, r = 0;
        if (root->left) l = root->left->val;
        if (root->right) r = root->right->val;

        if (l == 0)
            return min(f[r][0], min(f[r][1], f[r][2]) + 1);

        if (r == 0)
            return min(f[l][0], min(f[l][1], f[l][2]) + 1);

        int ans = N;
        ans = min(ans, f[l][0] + f[r][0]);
        ans = min(ans, f[l][0] + f[r][1]);
        ans = min(ans, f[l][1] + f[r][0]);
        ans = min(ans, f[l][1] + f[r][1] + 1);
        ans = min(ans, f[l][2] + f[r][2]);
        ans = min(ans, f[l][0] + f[r][2]);
        ans = min(ans, f[l][2] + f[r][0]);
        ans = min(ans, f[l][1] + f[r][2] + 1);
        ans = min(ans, f[l][2] + f[r][1] + 1);

        return ans;
    }
};