题目描述

给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。

样例

输入: amount = 5, coins = [1, 2, 5]
输出: 4
解释: 有四种方式可以凑成总金额:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1

输入: amount = 3, coins = [2]
输出: 0
解释: 只用面额2的硬币不能凑成总金额3。

输入: amount = 10, coins = [10] 
输出: 1

算法1

(动态规划) $O(n^2)$

经典的完全背包问题。

状态定义：
变量dp[i][j] = 利用前i 个硬币拼凑出j 面额的组合数

状态计算：
利用Leetcode 的官方题解来说明：
举一个例子：amount = 11，可用面值有 2 美分，5 美分和 10 美分。 请注意，数量是无限的。

基本情况： amount == 0.
amount == 0,此时不用使用硬币就能组合成0，所以组合情况为1.

拿第一个硬币：2 美分进行组合：

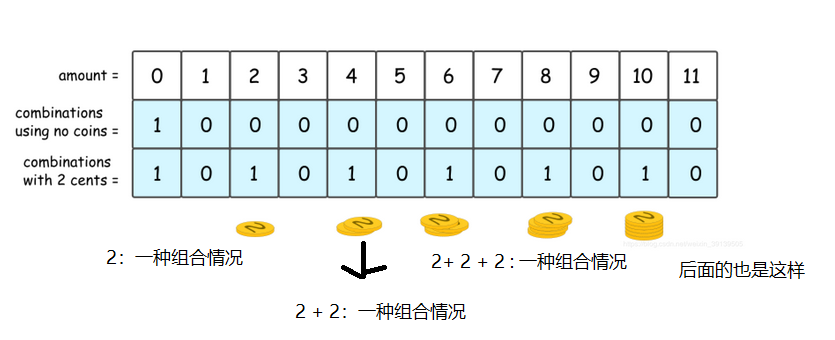
首先，amount金额小于 2 美分不会受到 2 美分的影响。 因此对于 amount = 0 和 amount = 1 的结果没有变化。

2 美分来组合 amount = 2，金额 2 美分的组合数 = 不使用2 美分组合成amount 的组合数 + 使用了2 美分组合成amount 的组合数
不使用当前2 美分就能组合成amount,就是使用了2 美分之前的硬币组合成的amount 的组合数。
使用了2 美分组合成amount, 就是amount - 2美分以后剩下的面额由剩下的硬币组合成的组合数。

同理 amount = 3 的组合数量等于 amount = 1 的组合数量，即 0。

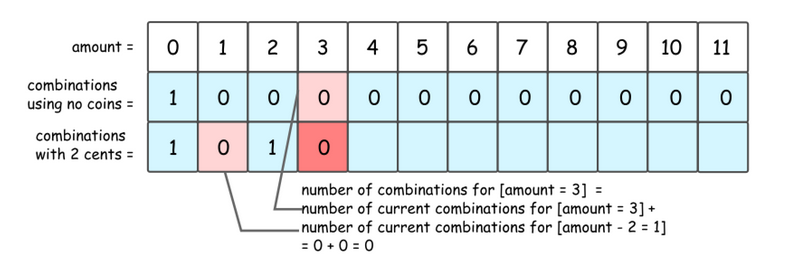
所以dp[i][j] = dp[i-1][j] + dp[i][j-coins[i]]
dp[i-1][j] : 代表只用i-1 以及之前的硬币就能凑出j 面额的组合数
dp[i][j - coins[i]]: 代表使用了当前硬币组合成的组合数,那么这个组合数 == j - coin[i] 的组合数。

因为dp[i][j] 只与dp[i-1][j] 和dp[i][j-coins[i]] 有关，我们可以把二维数组进行压缩，压缩成一维数组。
因为当我们在计算dp[i][j] 的时候, dp[i-1][j] 已经计算出来了。

时间复杂度

O(n^2)

参考文献

https://leetcode-cn.com/problems/coin-change-2/solution/ling-qian-dui-huan-ii-by-leetcode/

Java 代码

class Solution {
    public int change(int amount, int[] coins) {
        int n = coins.length,m = amount;
        int[] dp = new int[m + 1];
        dp[0] = 1;
        for(int i = 1; i <= n; i++){
        //当前零钱组合数都是基于count[i-2] 零钱(上一个零钱) 的组合数开始的
            for(int j = coins[i-1]; j <= amount; j++){
                dp[j] = dp[j] + dp[j - coins[i-1]];
            }
        }

        return dp[m];
    }
}