有依赖的背包问题的应用

有依赖的背包问题的模板可以参考 AcWing 10. 有依赖的背包问题 【存储边与边权值的方式与本题有所不同，所以初始化与状态转移方程会有所不同】

状态表示

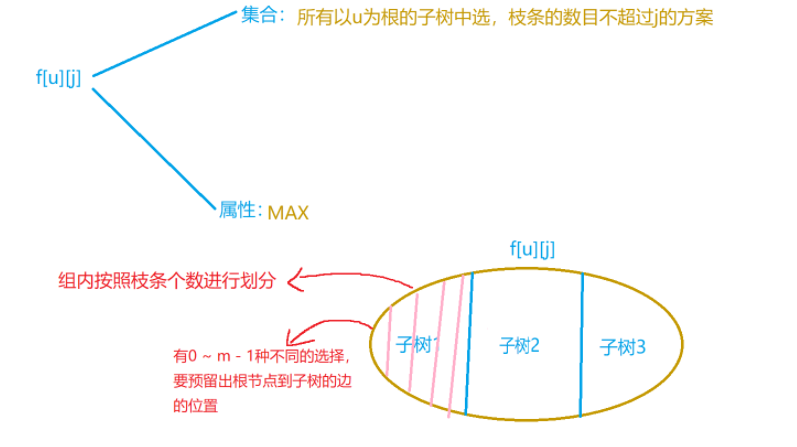
f[u][j]表示根节点为u，体积为j的所有选法中的最大价值

状态计算

每一棵子树看出一组背包，若需要选择该子树son，则根结点u到子树son的边一定用上，所以可以根据这一条边进行划分，所以是由(总变数 - 分组边数 - 1【f[u][j - k - 1]】）转移而来，(-1就是为了预留这条边的空间) ，因此能用上的总边数一定减1，总共可以选择j条边时，当前子树son分配的最大边数是j - 1，对于任意一棵子树有:

f[u][j] = Math.max(f[u][j], f[u][j - 1 - k] + f[son][k]+ w[i])

c++代码

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 110;
int e[2 * N],ne[2 * N],h[2 * N],w[2 * N],idx;  
int f[N][N];
//f[i][j]表示根节点为i的情况下使用枝条个数为j的最大数量
int n,m; //n表示树的节点数，k表示要保留的树枝数量

void add(int a,int b,int c){
    e[idx] = b;
    w[idx] = c;
    ne[idx] = h[a];
    h[a] = idx++; 
}

void dfs(int u,int father){  //因为是双向图,所以father的作用就是防止向下递归的时候到邻接回上面了

    for(int i = h[u];i != -1;i = ne[i]){
        if(e[i] == father)  continue;  //防止向上递归了


        dfs(e[i],u);
        //进行分组背包
        //枚举每一个分组(这里的是按照枝条个数进行分组，0 ~ m个枝条可以分成m个分组)
        for(int j = m;j >= 0;--j){
            //枚举分组内部的元素（最多只有j - 1个枝条，因为前提是[u~e[i]]的这个枝条要选）
            for(int k = 0;k <= j - 1;++k){ //这里要预留出u到j这一个枝条，因为选择节点e[j]的前提是u节点必须选上
                f[u][j] = max(f[u][j],f[u][j - k - 1] + f[e[i]][k] + w[i]);
            }
        }
    }
}

int main(){
    cin >> n >> m;
    memset(h,-1,sizeof h);
    for(int i = 1;i < n;++i){  //只有n - 1条边
        int a,b,c;
        cin >> a >> b >> c;
        //建树时没有标经方向，所以要建双向树
        add(a,b,c),add(b,a,c);
    }

    dfs(1,-1);
    cout << f[1][m] << endl;
    return 0;
}