类比于动态规划，使用d[x, y, state]表示的含义以及状态计算如下所示：

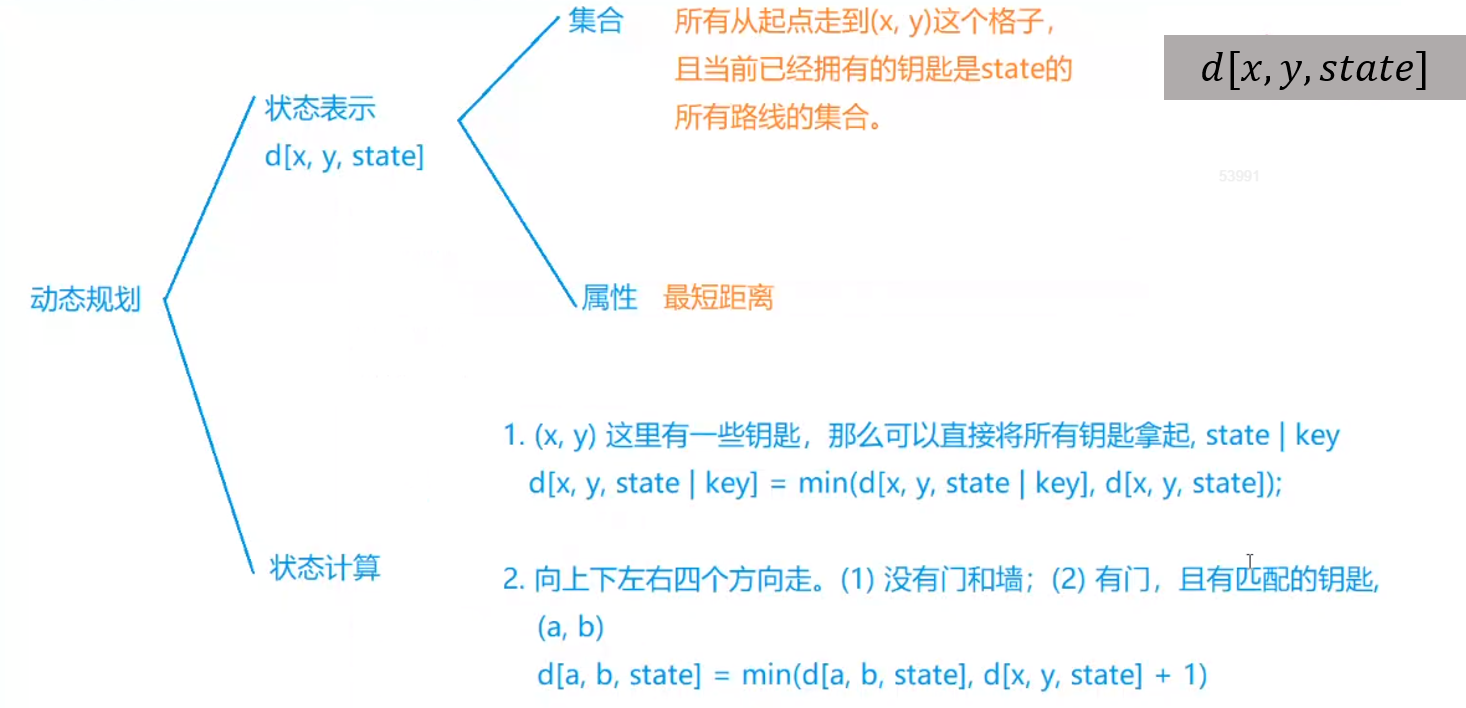
然而，这里的状态之间存在循环依赖（不存在拓扑序），比如对于迷宫中的位置[1, 3]与[1, 4]，它们之间由于不存在门而可以相互进入，则[1, 3, state]与[1, 4, state]之间就相互依赖，而导致无法计算。因此，本题不能用动态规划的方法来计算，而要转化成最短路问题来求解。

若要转化成最短路问题，关键是如何建图。根据上图中状态计算的分类，可通过如下方式建图：

• 将状态计算中的第1种情况看作是在[x, y, state]与[x, y, state | key]之间建立起一条边权为0的边;
• 将状态计算种的第2种情况看作是在[x, y, state]与[a, b, state]之间建立起一条边权为1的边；

补充知识点：
DP与最短路之间存在密切的联系，即DP问题可看作是拓扑图上的最短路问题，也就是说，如果存在拓扑序，最短路问题是可以用DP的方法来计算的，同样地，如果不存在拓扑序，则无法采用DP的方法来计算，而要类比成最短路问题来求解。

注意：为了简化代码，下面的代码中将方格[x, y]映射成一个整数，存储在g数组。

import java.util.*;

public class Main
{
    static int N = 12, M = N * N, P = N, E = 400, INF = 0x3f3f3f3f;
    static int[] h = new int[M];
    static int[] e = new int[E];
    static int[] ne = new int[E];
    static int[] w = new int[E];
    static int idx;
    static int n, m, p;
    static int[][] g = new int[N][N]; // 左上角(1, 1)对应图中编号为1的节点，节点编号从左到右、从上往下依序递增
    static int[] key = new int[M]; // key[x]表示图中编号为x的节点处，所拥有钥匙的状态（状态压缩）
    static int[][] d = new int[M][1 << P]; // d[id][state]表示从起点（即id=1）出发到id这个位置、所持钥匙状态是state时的最短路径
    static LinkedList<int[]> q = new LinkedList<>(); // 存储的是[id, state]，id表示图中节点编号，state表示所持钥匙的状态
    static boolean[][] st = new boolean[M][1 << P]; // 用于双端队列bfs，类似于dijkstra里的用于判断是否添加到集合中的数组
    static HashSet<String> edges = new HashSet<>(); // 存储添加了哪些边，图中节点编号3和7之间的边记作为“3 7”，其它情形类似
    static int[] dx = {-1, 1, 0, 0}, dy = {0, 0, -1, 1};

    public static void add(int a, int b, int c)
    {
        e[idx] = b;
        ne[idx] = h[a];
        w[idx] = c; // 存储的是门的类型
        h[a] = idx ++;
    }

    public static void build()
    {
        for(int i = 1; i <= n; i ++)
            for(int j = 1; j <= m; j ++)
                for(int u = 0; u < 4; u ++)
                {
                    int nx = i + dx[u], ny = j + dy[u];
                    if(nx <= 0 || nx > n || ny <= 0 || ny > m) continue;
                    StringBuilder e_sb = new StringBuilder();
                    e_sb.append(g[i][j] + " " + g[nx][ny]);
                    if(!edges.contains(e_sb.toString()))
                    {
                        add(g[i][j], g[nx][ny], 0);
                        edges.add(e_sb.toString());
                    }
                }
    }

    public static int bfs()
    {
        // 初始化d数组
        for(int i = 0; i < M; i ++) Arrays.fill(d[i], INF);
        // 初始化起点
        d[1][0] = 0;
        q.addLast(new int[]{1, 0});

        while(!q.isEmpty())
        {
            int[] t = q.removeFirst();
            if(st[t[0]][t[1]]) continue;
            st[t[0]][t[1]] = true;

            if(t[0] == n * m) return d[t[0]][t[1]];

            // 若有钥匙，则拿钥匙
            if(key[t[0]] != 0)
            {
                int nstate = t[1] | key[t[0]];
                d[t[0]][nstate] = Math.min(d[t[0]][t[1]], d[t[0]][nstate]);
                q.addFirst(new int[]{t[0], nstate});
            }

            // 向着四周（上下左右）转移
            for(int i = h[t[0]]; i != -1; i = ne[i])
            {
                int j = e[i];
                // 走不过去则跳过
                if(w[i] != 0 && (t[1] >> w[i] & 1) == 0) continue;
                // 可走过去
                if(d[j][t[1]] > d[t[0]][t[1]] + 1)
                {
                    d[j][t[1]] = d[t[0]][t[1]] + 1;
                    q.addLast(new int[]{j, t[1]});
                }
            }

        }

        return -1;
    }

    public static void main(String[] args)
    {
        Arrays.fill(h, -1);
        Scanner sc = new Scanner(System.in);
        n = sc.nextInt();
        m = sc.nextInt();
        p = sc.nextInt();
        // 初始化g数组
        for(int i = 1, t = 1; i <= n; i ++)
            for(int j = 1; j <= m; j ++)
                g[i][j] = t ++;

        // 建图
        int k = sc.nextInt();
        for(int i = 0; i < k; i ++)
        {
            int x1 = sc.nextInt(), y1 = sc.nextInt();
            int x2 = sc.nextInt(), y2 = sc.nextInt();
            int c = sc.nextInt();
            // 不是墙，就创建一条路径
            if(c != 0)
            {
                add(g[x1][y1], g[x2][y2], c);
                add(g[x2][y2], g[x1][y1], c);
            }
            StringBuilder e_sb1 = new StringBuilder();
            StringBuilder e_sb2 = new StringBuilder();
            e_sb1.append(g[x1][y1] + " " + g[x2][y2]);
            e_sb2.append(g[x2][y2] + " " + g[x1][y1]);
            edges.add(e_sb1.toString());
            edges.add(e_sb2.toString());

        }
        build();

        // 读取钥匙，特别注意同一方格处可能存在多把钥匙
        int s = sc.nextInt();
        for(int i = 0; i < s; i ++)
        {
            int x = sc.nextInt(), y = sc.nextInt(), q = sc.nextInt();
            key[g[x][y]] |= 1 << q;
        }

        // 利用双端队列bfs，求最短路的长度
        System.out.println(bfs());
    }
}