最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

本题给定一个数组 $\mathrm{a[N]}$，让我们求解两个量

1. 该数组的最长不上升子序列

2. 该数组最少能被几个最长下降子序列全部覆盖

样例的图例：

题解

对于第一问不再做过多赘述，关于如何求最长上升子序列模型DP，可以看之前的博客

这里主要说一下第二问的贪心思路及证明

第二题要求我们用最少的最长下降子序列对原数组进行全覆盖

考虑一种贪心方案：
对于第i个数来说，把它加入前 i - 1 个数构成的下降子序列组中，所有结尾元素大于第i个数的数中最小的那个数

证明：（最优解 = 贪心解）

假设存在一个最优解，他在考虑第 i 个数放入的下降子序列组中，选择了贪心解方案的后面的一个位置

具体如图所示：（绿色部分，更新了$q[i+1]$后为保证递增顺序，交换了$q[i]$和$q[i+1]$，这一步省略了）

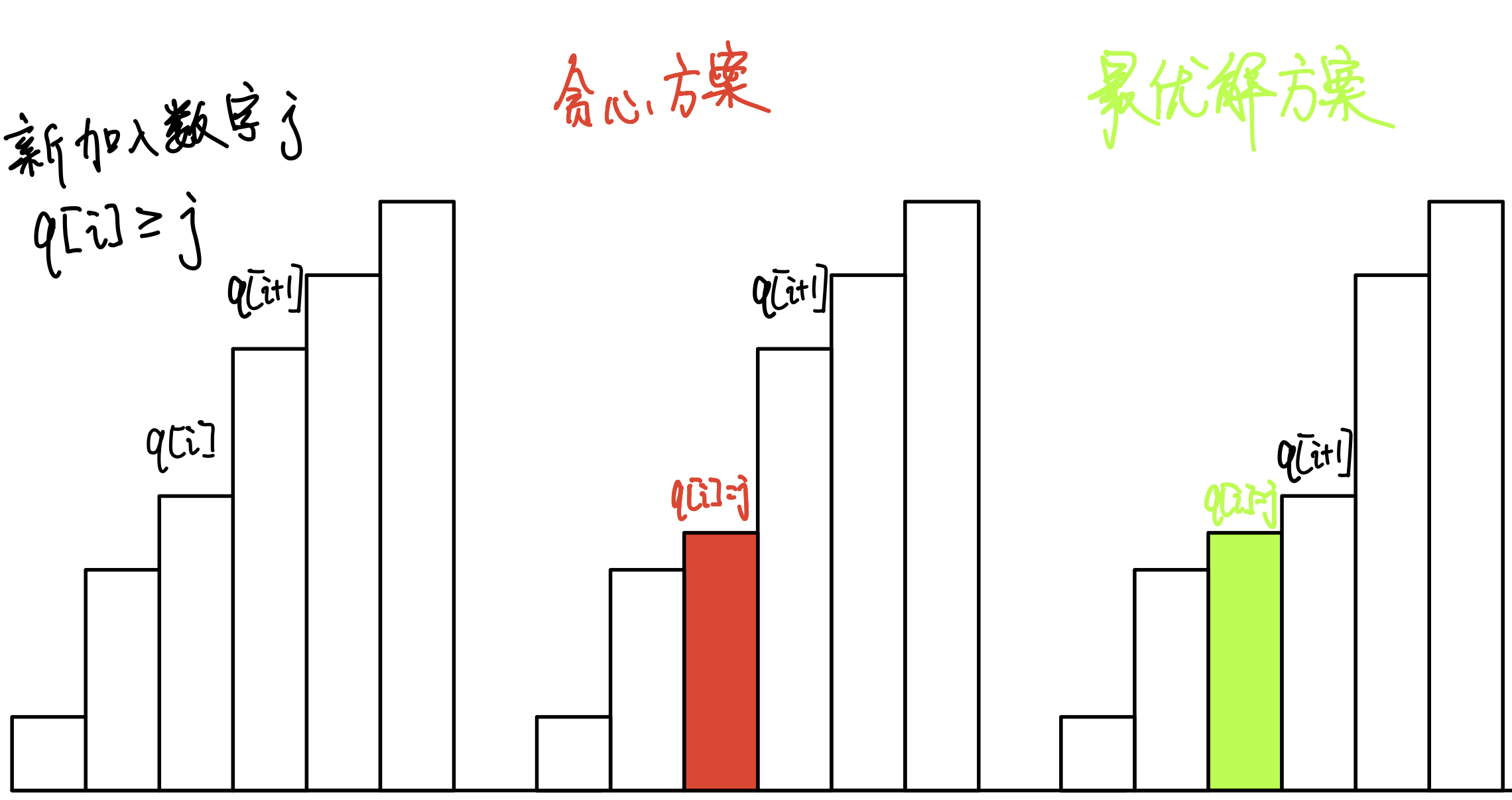
可以观察到，该最优策略使得当前局面差于贪心策略，即能接在$\big(q[i],q[i+1]\big)$范围的子序列少了一个

即贪心解 $\le$ 最优解

同理可证，最优策略在考虑第 i 个数放入的下降子序列组中，选择了贪心解方案的后面的第 $k$ 个位置
也有结论贪心解 $\le$ 最优解

此外，由于贪心解是合法解，所以必然 贪心解 $\ge$ 最优解

于是有 贪心解 $=$ 最优解

证明：（调整法）

假设存在一种最优策略，不是按照贪心方案进行阶段决策的

则我么可以通过有限次的调整，把最优解调整成贪心解的方案，具体如下图所示

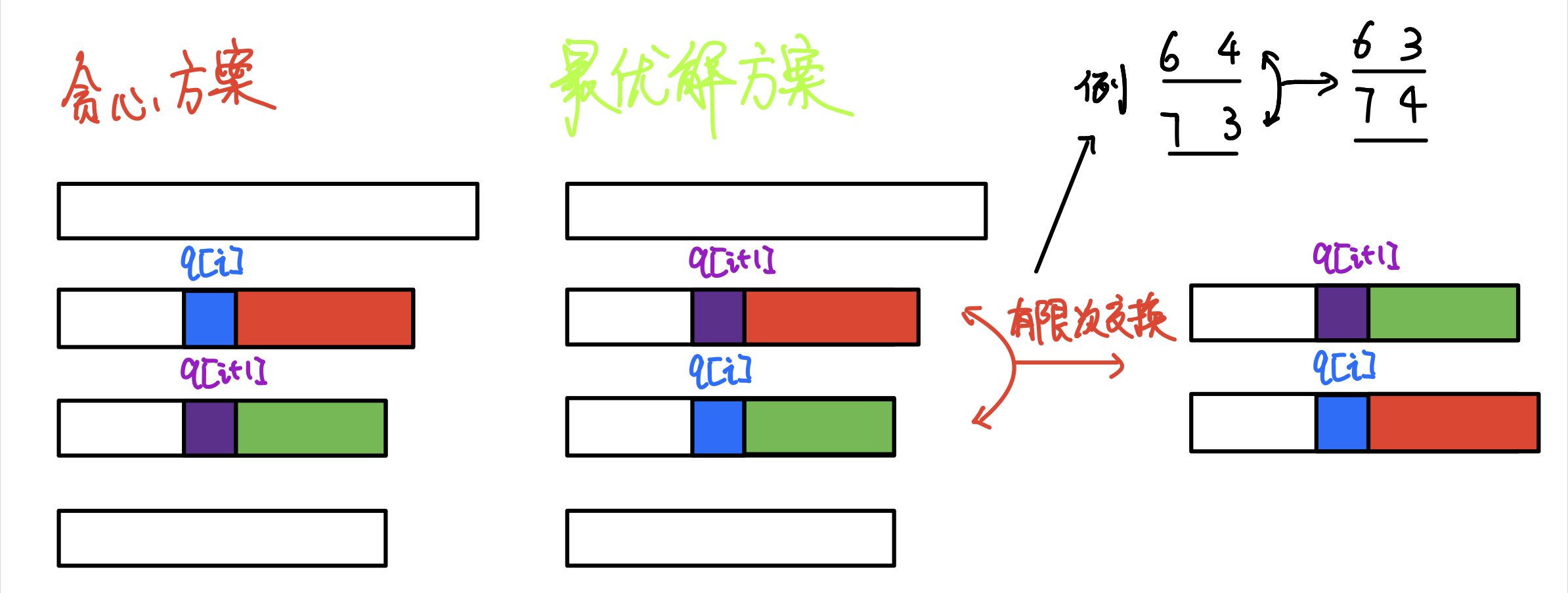
于是，由该决策包容性，得出最优解可以是贪心解。

Code

从前往后做一遍最长下降子序列，同时维护一个数组长度为$\mathrm{cnt}$的单调不减数组$\mathrm{q[N]}$

数组 q[N] 中每个元素维护的是当前以 q[i] 结尾的下降子序列

于是，对于第 i 个元素来说，他能插入的到 q[N] 中的哪个下降子序列中，是存在一个二分性质的

由于要求的是下降子序列且 q[N] 是单调不减的

因此对于所有的 w[i] ，必然存在一个边界 j ，满足$\forall k \in [0,j),有q[k] < w[i]$ 且 $\forall k \in [j,cnt],有w[i] \le q[k]$

于是我们就可以用二分来优化找满足性质：$w[i] \ge q[k]$ 的区间左端点即可

具体代码如下：（此题考的主要是这个贪心，对于前面的DP较为简单，因此不画闫氏DP分析法了）

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010, INF = 30010;

int n, x;
int w[N], f[N];
int q[N], cnt;

int main()
{
    while (cin >> x) w[ ++ n] = x;
    //对于第一问，先做一遍最长上升子序列模型DP
    int res = 0;
    w[0] = INF;
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j < i; ++ j)
        {
            if (w[j] >= w[i]) f[i] = max(f[i], f[j] + 1);
        }
        res = max(res, f[i]);
    }
    cout << res << endl;

    //对于第二问，我们采用题解中所说的贪心思路
    for (int i = 1; i <= n; ++ i)
    {
        int l = 0, r = cnt; //二分出插入的区间左端点
        while (l < r)
        {
            int mid = l + r >> 1;
            if (q[mid] >= w[i]) r = mid;    //右边的性质满足q[k] >= w[i]
            else l = mid + 1;
        }
        if (q[r] < w[i]) r ++ ; //处理边界，当没有能够满足当前高度的系统时，再开一个
        cnt = max(cnt, r);
        q[r] = w[i];
    }
    cout << cnt << endl;
    return 0;
}