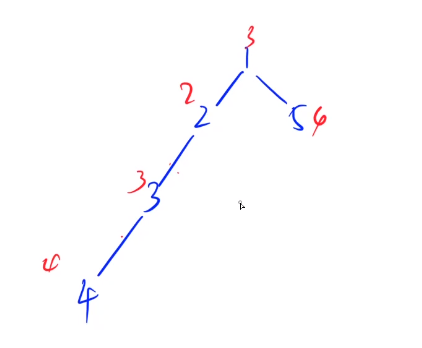
树形dp求解树的中心模板题

题目样例：

核心：

可以将问题转化成求一遍当前节点的向下最长路径和向上最长路径

求解向下的路径长度过程与 AcWing 1072. 树的最长路径 基本相同

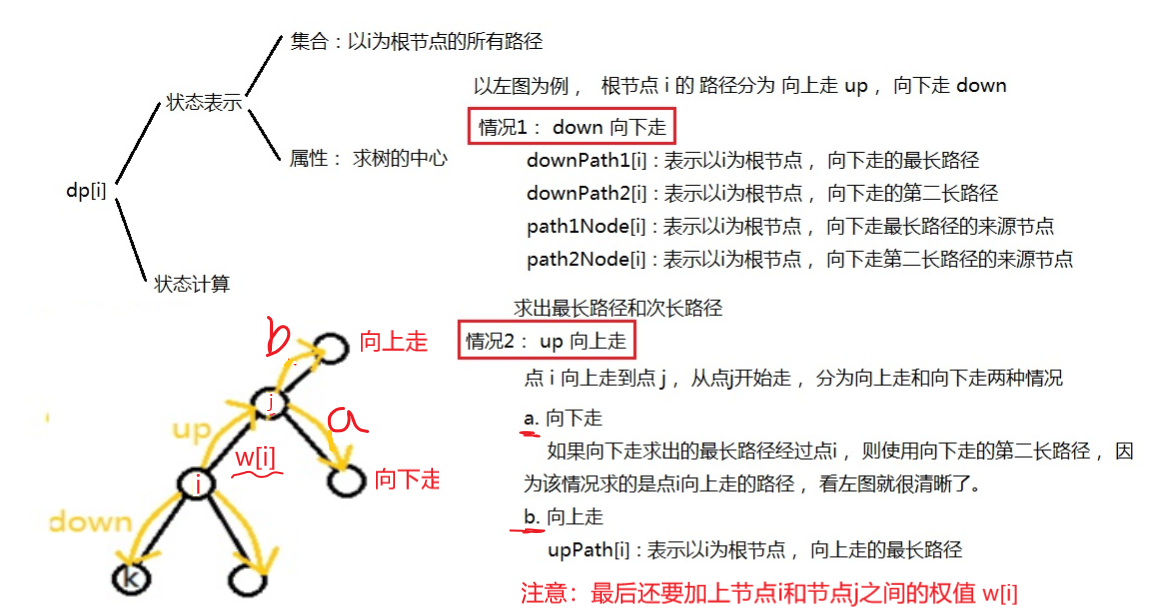
void dfs_up(int u,int father){ //father的用法与上面相同
    for(int i = h[u];i != -1;i = ne[i]){
        int j = e[i];
        if(j == father) continue;
        //当节点u的向下的最长路径是沿j向下得到的，但是现在计算的是向上的路径，所以不能重复计算相同的一条路径。
        //所以要选择次长的路径
        if(pm[u] == j) up[j] = max(d2[u],up[u]) + w[i];
        else up[j] = max(d1[u],up[u]) + w[i];
        dfs_up(j,u);//用j更新j的子节点的最长向上距离
    }
}

最后再遍历一遍所有节点求解每个节点到其他节点的最长距离,然后将其中的最小值记录下来即可

c++代码

因为计算的是一个分支的最长路径，所以不存在两个路径同时占用一个根节点的情况

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 10010;
int h[2 * N],ne[2 * N],e[2 * N],w[2 * N],idx; //邻接表存储树节点，idx为节点的指针值
int d1[N],d2[N]; 
//d1[u]表示节点u向下走的路径的最大长度；d2[u]表示节点u向下走的路径的次大长度
int up[N];
//up[u]表示节点u向上走的路径的最大长度
int pm[N]; //pm[u]记录u沿哪个节点向下走可以的到最长的向下路径
int n;


void add(int a,int b,int c){
    w[idx] = c;
    e[idx] = b;
    ne[idx] = h[a];
    h[a] = idx++;
}

//因为计算的是一个分支的最长路径，所以不存在两个路径同时占用一个根节点的情况
int dfs_down(int u,int father){ //因为是无向图，用father记录当前节点u的根节点，防止向下走的时候下一个节点又邻接到上一个节点去了

    d1[u]=d2[u]=-0x3f3f3f3f;

    for(int i = h[u];i != -1;i = ne[i]){

        int j = e[i];
        if(j == father) continue;
        int dist = dfs_down(j,u) + w[i]; //dist表示当前节点沿节点j向下走的最大路径长度
        if(dist >= d1[u]){
            //注意这里的赋值顺序不能反
            d2[u] = d1[u];
            d1[u] = dist;
            pm[u] = j;
        }else if(dist > d2[u]) d2[u] = dist;
    }
    if(d1[u]==-0x3f3f3f3f) d1[u]=d2[u]=0;//如果值没有更新的话表示该节点为叶子节点(末节点)

    return d1[u]; //返回最大值
}

void dfs_up(int u,int father){ //father的用法与上面相同
    for(int i = h[u];i != -1;i = ne[i]){
        int j = e[i];
        if(j == father) continue;
        //当节点u的向下的最长路径是沿j向下得到的，但是现在计算的是向上的路径，所以不能重复计算相同的一条路径。
        //所以要选择次长的路径
        if(pm[u] == j) up[j] = max(d2[u],up[u]) + w[i];
        else up[j] = max(d1[u],up[u]) + w[i];
        dfs_up(j,u);//用j更新j的子节点的最长向上距离
    }
}


int main(){
    cin >> n;
    memset(h,-1,sizeof h);
    for(int i = 1;i < n;++i){   //一共有n - 1条边
        int a,b,c; 
        cin >> a >> b >> c;
        add(a,b,c),add(b,a,c);
    }

    dfs_down(1,-1);
    dfs_up(1,-1);


    //节点编号从1开始
    int res=d1[1];//因为根节点没有向上的路径，所以 

    for(int i = 2;i <= n;++i){
        res = min(res,max(d1[i],up[i]));
        //因为本题数据中1<=c<=100000,没有负权边,所以不需要特判子叶节点的向下的路径不存在的情况
    }
    cout << res << endl;
    return 0;
}