最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

本题定义了一个上升子序列和：对于元素满足从左往右数值递增的次序的子序列的和

我们要求出该序列中最大上升子序列和

题解

该题目定义的最大上升子序列模型与我们熟悉的最长上升子序列模型非常相似

因此我们可以采用最长上升子序列DP模型来分析本题

时间复杂度：$O(n^2)$

闫氏DP分析法

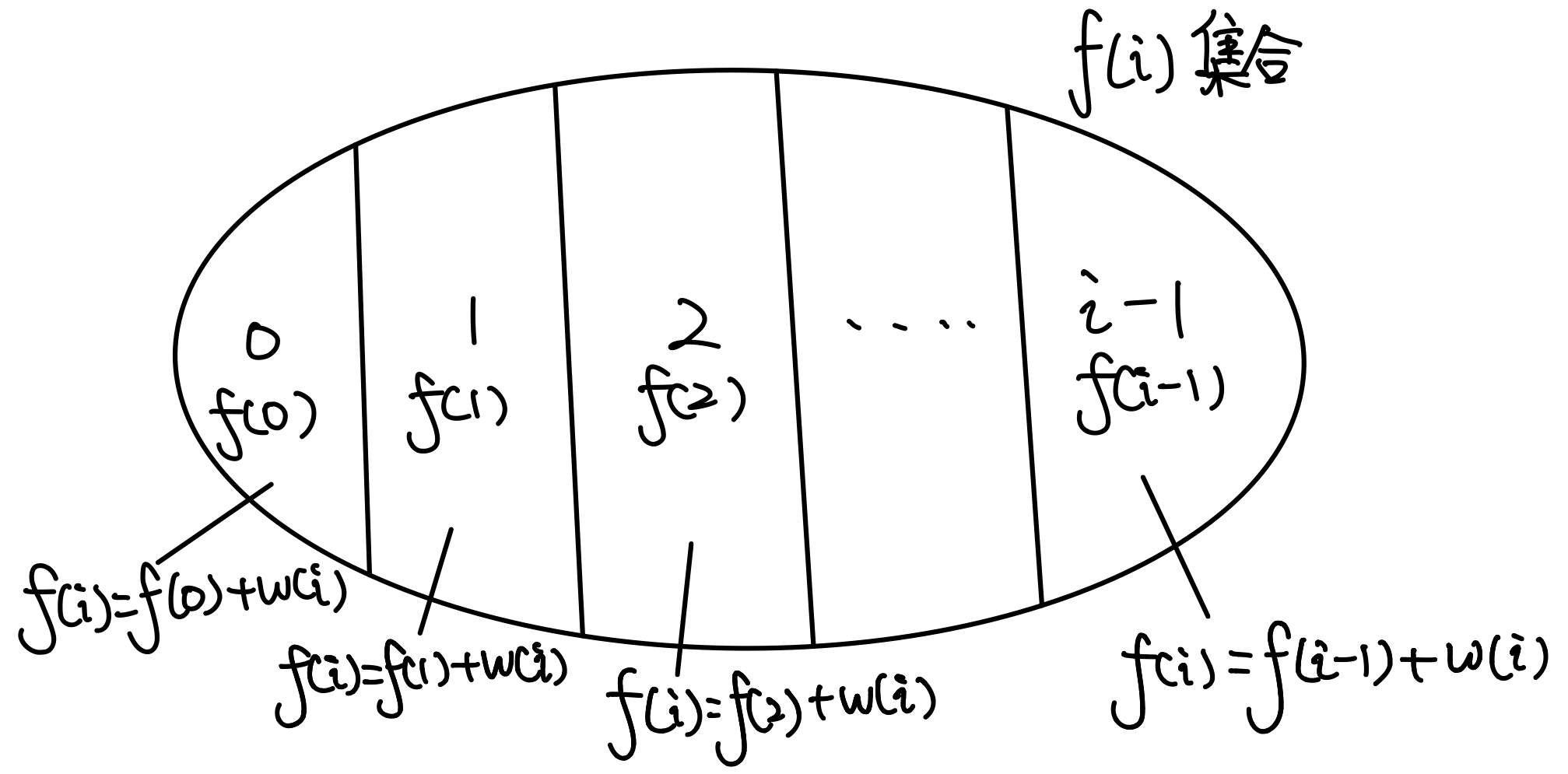
状态表示 $f_i$: 考虑前i个元素，以第i个元素结尾的最大上升子序列的方案

状态属性: 最大上升子序列和最大 $\mathrm{Max}$

状态转移: $f_i = \sum_{j=0}^{i-1}f_j + w[i] \quad (满足w[i] > w[j]才能转移)$

集合划分:

Code:

#include <iostream>

using namespace std;

const int N = 1010;

int n;
int w[N];
int f[N];

int main()
{
    //input
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> w[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j <= n; ++ j)
        {
            if (w[i] > w[j])
            {
                f[i] = max(f[i], f[j] + w[i]);
            }
        }
    }

    //find res
    int res = 0;
    for (int i = 1; i <= n; ++ i) res = max(res, f[i]);

    //output
    cout << res << endl;

    return 0;
}