莫比乌斯函数:

1. 该函数对应的实际问题：
容斥原理==>求1~n中与n互质的数

n - (n/2) - (n/3) - (n/5) - (n/7) - ... - (n/pk)
  + (n/6) + (n/10) + (n/14) + ... + (n/pk-1pk)
  -...
  +...

n/t 表示1~n中t的倍数的个数
每个(n/t)前面的系数由t决定，所以定义出了莫比乌斯函数，从而可以直接确定t的倍数个数的系数

由于是根据上述表达式进行定义的，所以上式中未出现的项，根据定义系数为0，如(n/4)等

2. 求取
可通过筛质数的方法进行确定 

关于本题

1. 问题转换
原问题：给出a, b, d
求当1 <= x <= a, 1 <= y <= b
(x, y) = d的数对个数
==> (x/d, y/d) = 1

问题转化为当1 <= x <= a/d, 1 <= y <= b/d
(x, y)互质的数对个数

2. 如何求
首先令a /= d, b /= d。
在1~a和1~b中去掉最大公因数大于1的数，rest_a * rest_b即为所求。

利用容斥原理曲线救国：
a, b的最大 可能 公因数n = min(a, b)
a * b - (a/2) * (b/2) - (a/3) * (b/3) - ...
      + (a/6) * (b/6) + (a/10) * (b/10) + ...
      - ...
      + ...

此时可供选择的做法有
(1). 筛质数 + 指数型枚举的容斥原理
时间复杂度分析：< n的质数个数即为 指数枚举的位数，必然超时
(2). 根据莫比乌斯函数实现O(n)时间求解，询问数50000 * n(最大取50000) 超时

发现虽然有n项，但是a/t只有 2*sqrt(a)个值，即2*sqrt(a)段

证明：
a/1 ~ a/sqrt(a)共sqrt(a)项
a/sqrt(a) + 1 ~ a/a共sqrt(a)个值
故最多有2*sqrt(a)个值

于是尝试对方法(2)进行优化，即一次求尽可能长的一段l <= t <= r
(a/t)都相等，(b/t)都相等，如此可以一次跳一段，
时间复杂度 < sqrt(a) + sqrt(b) < 2sqrt(50000)
可以过

3. 如何保证一次跳跃是最大的
常数a固定
定义g(x)函数：g(x) = (int)a / (int)(a / x)

性质：
(1). (int)a/x = (int)a/g(x)
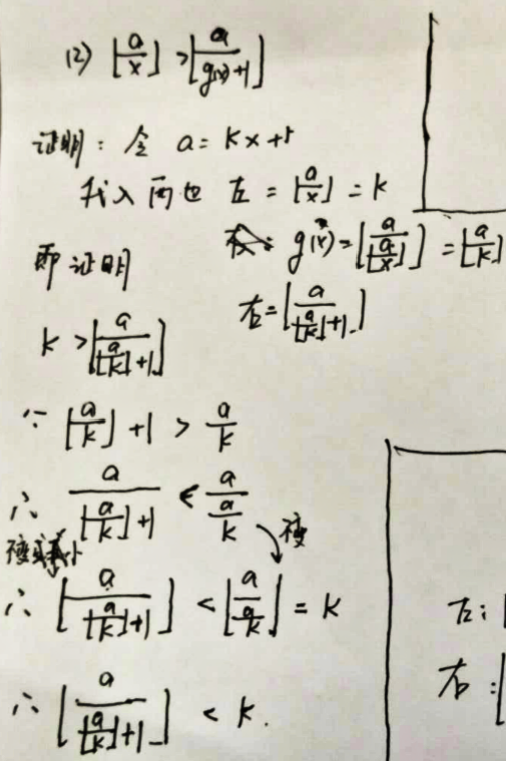
(2). (int)a/x > (int)a/(g(x)+1)
如a = 24, 则g(9) = g(10) = g(11) = g(12) = 12
g(x)表示本段的右边界，g(x) + 1表示下一段的左边界

满足(1), (2)两个性质即可实现每次跳到本段右端点

关于两条性质的证明

(1)

(2)

代码

#include<iostream>

using namespace std;

typedef long long LL;

const int N = 50010;

int T;
int primes[N], cnt;
bool st[N];
int mobius[N], s[N];

void init(int n) {
    mobius[1] = 1;
    for (int i = 2; i <= n; ++i) {
        if (!st[i]) {
            primes[cnt++] = i;  // 质数 只含一个 质数
            mobius[i] = -1;
        }

        for (int j = 0; primes[j] * i <= n; ++j) {
            int t = primes[j] * i;
            st[t] = true;
            if (i % primes[j] == 0) {  // p[j]已经在i中出现，指数>1
                mobius[t] = 0;
                break;
            }
            mobius[t] =  mobius[i] * -1;  // p[j]在i中未出现过，t中质数种类+1
        }
    }
    // 一段区间的a / i和b / i是相同的，所以只需要将系数累加即可
    for (int i = 1; i <= n; ++i) s[i] = s[i - 1] + mobius[i];
}

int main() {
    init(N - 1);
    scanf("%d", &T);
    while (T--) {
        int a, b, d;
        scanf("%d %d %d", &a, &b, &d);
        a /= d, b /= d;
        int n = min(a, b);

        LL res = (LL)a * b;
        for (int l = 2, r; l <= n; l = r + 1) {
            int gar = a / (a / l);  // 与a / l相同的最大的r
            int gbr = b / (b / l);
            int ne = min(gar, gbr);
            r = min(n, ne);

            res = res + ((LL)s[r] - s[l - 1]) * (a / l) * (b / l);
        }
        printf("%lld\n", res);
    }
    return 0;
}