首先我们需要注意的是子序列,子序列不需要连续。子串是需要是连续的,子序列不需要。

我们分析出，最优解具有的性质。

${1111}^{S1} \ {2222}^{S2} \ {1111}^{S3} \ {2222}^{S4}$

在y总的分析下，我们得到了4个状态，状态的属性是最大长度，而这4个状态的转移如下

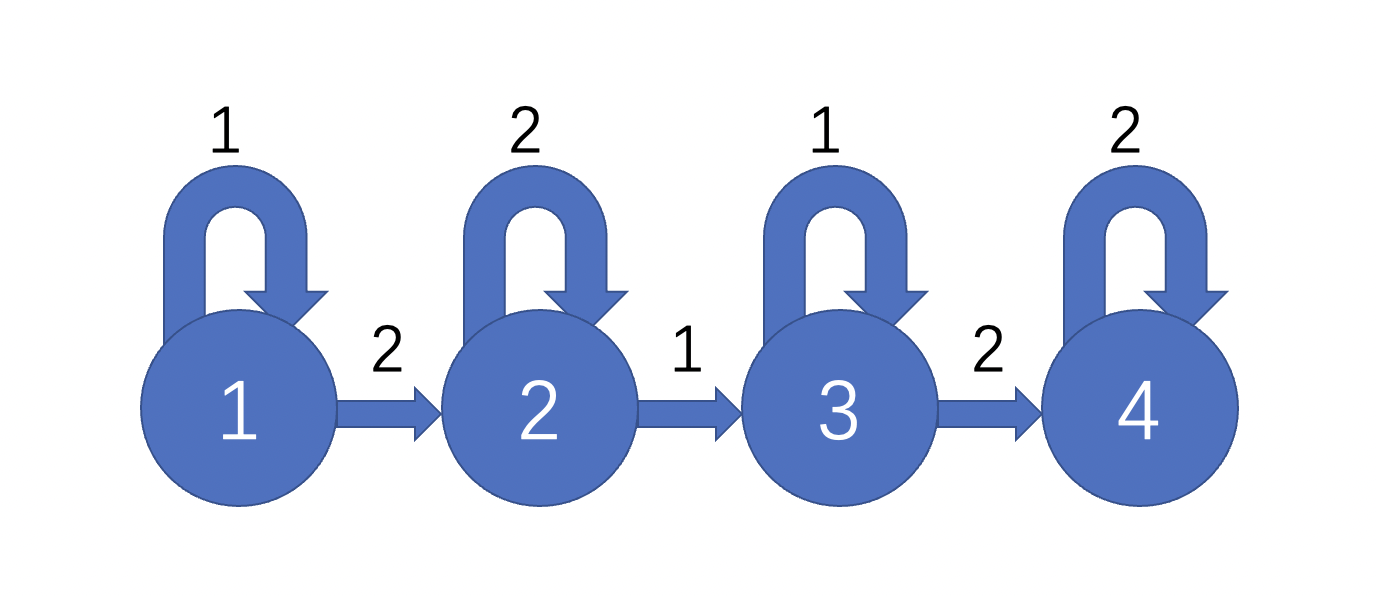
然后进行遍历，遍历过程中进行状态转移。

当遍历遇到的数为1时

• 1状态可以更新
• 3状态可以由2状态转移，也可以3状态本身转移过来。两种转移方式取最大$max(S2+1,S3+1)$

当遍历遇到的数为2时

• 2状态可以由1状态转移过来，也可以2状态本身转移过来。两种转移方式取最大$max(S1+1,S2+1)$
• 4状态同理可以由3状态转移过来，也可以由4状态本身转移过来。两种状态取最大$max(S3+1,S4+1)$

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
//1 2 1 2
int main()
{
    int n;
    scanf("%d", &n);

    int s1=0,s2=0,s3=0,s4=0;

    while (n -- )
    {
        int x;
        scanf("%d", &x);

        if(x==1)
        {
            s1=s1+1;

            s3=max(s3+1,s2+1);
            //cout<<s1<<' '<<s2<<' '<<s3<<' '<<s4<<' '<<endl;

        }
        else
        {
            s2 = max(s1+1,s2+1);
            s4 = max(s3+1,s4+1);
        }
    }

    printf("%d\n",max(s3,s4));
    return 0;
}

Ps：理论上最后输出$max(S1,S2,S3,S4)$，绝对没有错。但是可以通过简单证明$S3 \ge S1,S4 \ge S2$。只需要比较$S3,S4$即可。举个例子：比如当序列全部是1，$S3$状态就等价于$S1$，$S4$状态等价于$S2$。