题目描述
一条包含字母 A-Z 的消息通过以下映射进行了 编码 :
‘A’ -> 1
‘B’ -> 2
…
‘Z’ -> 26
要 解码 已编码的消息,所有数字必须基于上述映射的方法,反向映射回字母(可能有多种方法)。例如,”11106” 可以映射为:
"AAJF" ,将消息分组为 (1 1 10 6)
"KJF" ,将消息分组为 (11 10 6)
注意,消息不能分组为 (1 11 06) ,因为 “06” 不能映射为 “F” ,这是由于 “6” 和 “06” 在映射中并不等价。
给你一个只含数字的 非空 字符串 s ,请计算并返回 解码 方法的 总数 。
题目数据保证答案肯定是一个 32 位 的整数。
样例
输入:s = "12"
输出:2
解释:它可以解码为 "AB"(1 2)或者 "L"(12)。
输入:s = "226"
输出:3
解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
输入:s = "0"
输出:0
解释:没有字符映射到以 0 开头的数字。
含有 0 的有效映射是 'J' -> "10" 和 'T'-> "20" 。
由于没有字符,因此没有有效的方法对此进行解码,因为所有数字都需要映射。
输入:s = "06"
输出:0
解释:"06" 不能映射到 "F" ,因为字符串含有前导 0("6" 和 "06" 在映射中并不等价)。
算法1
(动态规划) $O(n^2)$
如何发现它是动态规划?
题目中给到的信息: 字符串s 的某个i 位置而言,位置i 只与自己能否形成一个一位数去解码亦或者位置i 与位置i - 1 能否形成一个两位数去进行解码. 与其他的位置字符都没有关系
状态变量:
变量dp[i] 代表从0 到i 位置的字符。 属性: 解码的数量. 所以dp[i] 就是代表从0 到i 位置的字符解码的数量
状态计算:
‘12’,‘121’,‘1212’ 的组合数量:
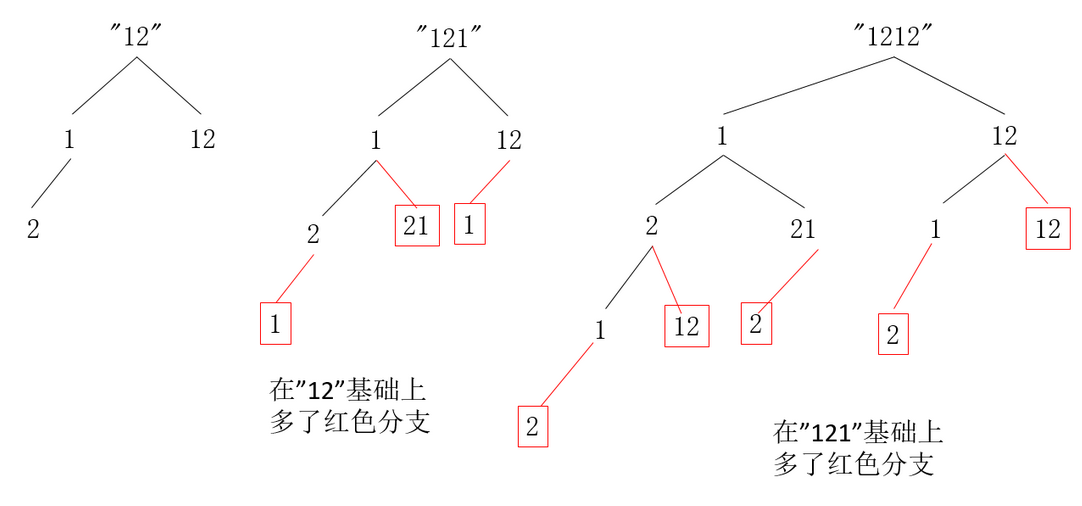
1212最后一个数字2不等于0,可以单独编码,也可以跟前面一个数字组合在一起(12)编码,所以:
1212的编码数量 等于 12的数量 + 121的数量
所以dp[i] = dp[i-1] + dp[i-2]
但是如果当前i 位置的字符是‘0’ 或者当前i 位置 与i - 1位置字符组成两位数时, i - 1位置的字符是‘0’ 的话,那都不能成为答案.并且得出来的两位数字符必须 <= 26.
时间复杂度
O(n)
参考文献
https://leetcode-cn.com/problems/decode-ways/solution/san-chong-jie-fa-xiang-xi-tu-jie-91-jie-6vh2k/
Java 代码
class Solution {
public int numDecodings(String s) {
if(s.charAt(0) == '0') return 0;
int n = s.length();
if(n == 1){
return s.charAt(n - 1) == '0'? 0:1;
}
int[] dp = new int[n];
//能从上面出来这里,说明n > 1
//并且第一位 != '0'
dp[0] = 1;
if(s.charAt(1) != '0'){
dp[1] = 1;
}
if(s.charAt(0) != '0' && ((s.charAt(0) - '0') * 10 + (s.charAt(1) - '0')<= 26)){
dp[1] += dp[0];
}
for(int i = 2; i < n; i++){
if(s.charAt(i) != '0'){
dp[i] += dp[i-1];
}
if(s.charAt(i-1) != '0' && ((s.charAt(i-1) - '0') * 10 + (s.charAt(i) - '0')<= 26)){
dp[i] += dp[i-2];
}
}
return dp[n-1];
}
}
简化版本:
注意: 此时的dp[0] = 1 代表: 空字符串s可以有 1 种解码方法,解码出一个空字符串。
public class 解码方法 {
public int numDecodings(String s) {
int n = s.length();
int[] dp = new int[n + 1];
dp[0] = 1;
for(int i = 1; i <= n; i++){
if(s.charAt(i-1) != '0'){
dp[i] += dp[i-1];
}
if(i > 1){
if(s.charAt(i-2) != '0' && ((s.charAt(i-2) - '0') * 10 + (s.charAt(i-1) - '0')<= 26)){
dp[i] += dp[i-2];
}
}
}
return dp[n];
}
}
优化:
因为dp[i] 只与dp[i-1] 和dp[i-2] 有关,所以我们可以不使用数组,改用3个变量来记录dp[i-1] ,dp[i-2] ,dp[i].
class Solution {
public int numDecodings(String s) {
int n = s.length();
//dp[0] = 1: 空字符串s 也能解析出1 中空字符解码
int lastLast = 0;
int last = 1;
for(int i = 1; i <= n; i++){
int cur = 0;
if(s.charAt(i-1) != '0'){
cur += last;
}
if(i > 1){
if(s.charAt(i-2) != '0' && ((s.charAt(i-2) - '0') * 10 + (s.charAt(i-1) - '0')<= 26)){
cur += lastLast;
}
}
lastLast = last;
last = cur;
}
return last;
}
}
算法2
(递归 + 记忆化) $O(n)$
检验每个字符以及与它后面一个字符进行组合以后能否进行解码,那这个过程可以使用递归.
以下为别人的笔记图解:
以121为例:
可以先解码1变成A、再是2变成B,最后是1解码为A
也可以先编码1、再是21解码为U
或者先编码12为L,再编码1
所以,一共有3种编码方式:
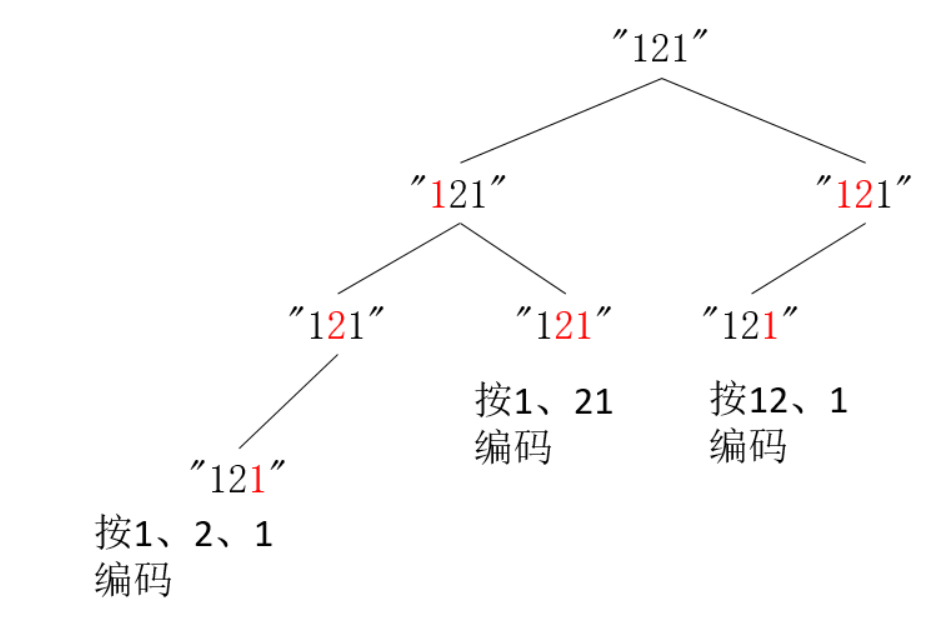
从上图中,可以发现,这种分解方式跟爬楼梯很类似,可以一次爬一个台阶、或者一次爬两个台阶。
即:一次编码一个数字、或者一次编码两个数字。
所不同的是,这题编码的时候,需要附加很多判断条件。比如:
单个字符是0就没法编码了
两个字符是27这也没法编码
所以,我们要先检查一位、两位的字符是否在合法范围内,如果是合法范围内,再递归的进行编码。
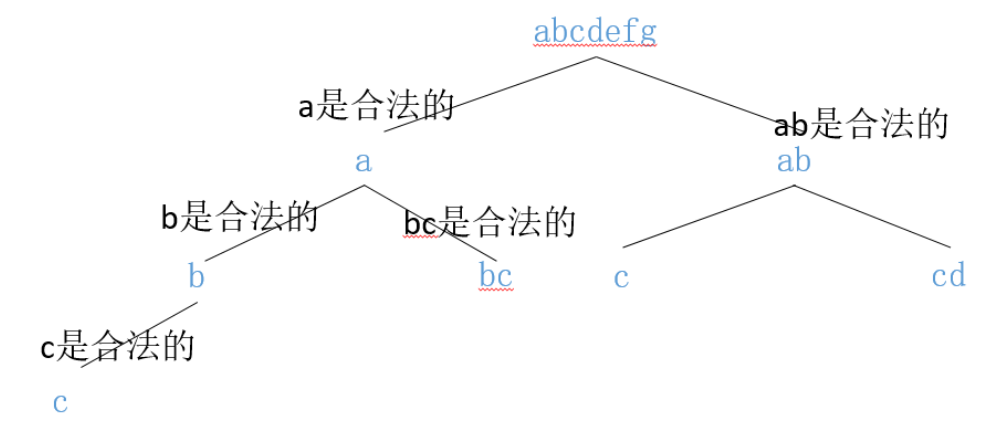
如上图,每次检测一位、两位是否合法,再递归处理
所以最坏的情况下时间复杂度是 O(2N)O(2^N)O(2N) 这个级别的,当然我们加个缓存就可以把时间给降下来了。
时间复杂度:O(N)
空间复杂度:O(N)
时间复杂度
O(n)
参考文献
https://leetcode-cn.com/problems/decode-ways/solution/san-chong-jie-fa-xiang-xi-tu-jie-91-jie-6vh2k/
Java 代码
class Solution {
public int numDecodings(String s) {
if(s.charAt(0) == '0') return 0;
return helper(new HashMap(),s,0);
}
public int helper(Map<Integer,Integer> map,String s,int index){
//能进入到递归的,前提都是: s.charAt(index) != '0',那只要当前index 字符 != 0,就必然会有1 个解.
//而这个解其实是对应最开始的index = 0 时的字符的解. 因为后面的res 都是以index + 1 开始的解.
if(index >= s.length()) return 1;
if(map.containsKey(index)){
return map.get(index);
}
int res = 0;
if(s.charAt(index) != '0'){
res += helper(map,s,index + 1);
}
if(s.charAt(index) != '0' && index + 1 < s.length() && (s.charAt(index) == '1' || s.charAt(index) == '2' && s.charAt(index + 1) <= '6')){
res += helper(map,s,index + 2);
}
map.put(index,res);
return res;
}
}

