题目描述

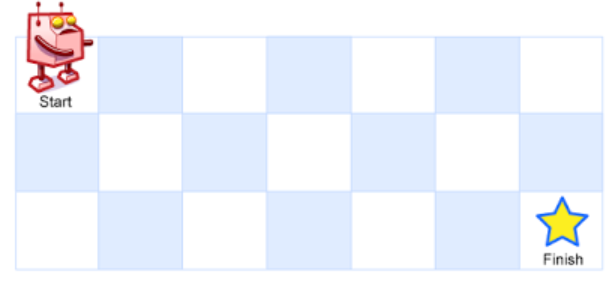
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

样例

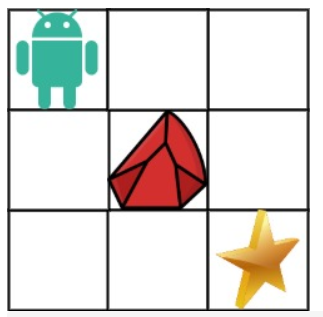
输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

算法1

(动态规划) $O(n^2)$

怎么知道这题是用动态规划来解？
我觉得用Leetcode 官方的话来解释挺好的:
我们需要从问题本身出发，寻找一些有用的信息，例如本题中：
(i,j) 位置只能从 (i−1,j) 和 (i,j−1) 走到，这样的条件就是在告诉我们这里转移是「无后效性」 的，f(i,j) 和任何的 f(i′,j′)(i′>i,j′>j) 无关。

动态规划的题目分为两大类，一种是求最优解类，典型问题是背包问题，另一种就是计数类，比如这里的统计方案数的问题，它们都存在一定的递推性质。前者的递推性质还有一个名字，叫做 「最优子结构」 ——即当前问题的最优解取决于子问题的最优解，后者类似，当前问题的方案数取决于子问题的方案数。所以在遇到求方案数的问题时，我们可以往动态规划的方向考虑。

通常如果我们察觉到了这两点要素，这个问题八成可以用动态规划来解决。

再来说说解题思路:
状态变量:
变量dp[i][j] 代表从起点开始到(i,j) 的路径. 属性: 路径数量. 所以dp[i][j] 表示从起点开始到(i,j) 的路径数量.

状态计算:
题目中给到条件: 只能往右,下两个方向走.所以dp[i][j] = dp[i-1][j] + dp[i][j - 1].
但是在第一行的时候,是没有上一行的,所以此时: dp[i][j] += dp[i][j-1]
在第一列的时候,是没有左边一列的,所以此时: dp[i][j] += dp[i-1][j]

初始条件:
dp[0][0] = 1;

时间复杂度

O(n^2)

参考文献

https://leetcode-cn.com/problems/unique-paths-ii/solution/bu-tong-lu-jing-ii-by-leetcode-solution-2/

Java 代码

    public int uniquePathsWithObstacles(int[][] nums) {
        int n = nums.length,m = nums[0].length;
        int[][] dp = new int[n][m];
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(nums[i][j] == 1) continue;
                if(i == 0 && j == 0) dp[i][j] = 1;
                if(i > 0) dp[i][j] += dp[i-1][j];
                if(j > 0) dp[i][j] += dp[i][j-1];
            }
        }
        return dp[n-1][m-1];
    }

另一种写法:
使 dp[i][j] = dp[i-1][j] + dp[i][j-1] 更加通用. 因为从第一行一直往右走,和从第一列一直往下走都是一条路线,所以把dp先预处理dp[0][j] 和dp[i][0] , 那么后面的遍历就都从第二行第二列开始.

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        // 定义 dp 数组并初始化第 1 行和第 1 列。
        int m = obstacleGrid.length, n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
            dp[i][0] = 1;
        }
        for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
            dp[0][j] = 1;
        }

        // 根据状态转移方程 dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 进行递推。
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 0) {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m - 1][n - 1];
    }
}

算法2

(动态规划 + 空间优化) $O(n^2)$

因为dp[i][j] 只与dp[i-1][j] 和dp[i][j-1] 有关,也就是求第i行时，只需要i-1行已求解过的值，不需要i-2行的了。
所以这里可以用滚动数组进行优化，将二维数组改为一维数组,这个一维数组的大小与nums[0].length 相同.

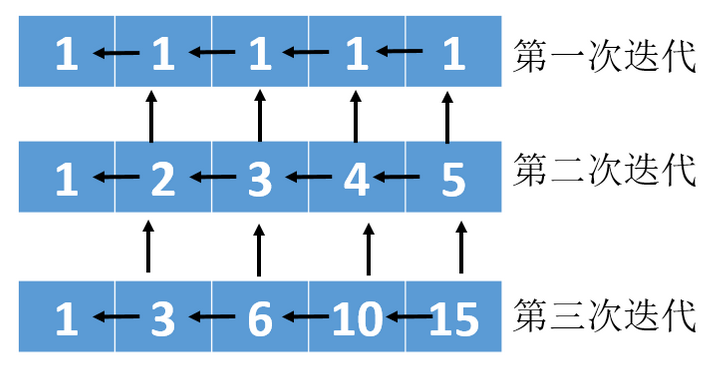
计算当前值 = 以求出的左边值 + 上一次迭代同位置的值
dp[j] = dp[j - 1] + dp[j]

时间复杂度

O(n^2)

参考文献

https://leetcode-cn.com/problems/unique-paths-ii/solution/bu-tong-lu-jing-ii-by-leetcode-solution-2/

https://leetcode-cn.com/problems/unique-paths-ii/solution/si-chong-shi-xian-xiang-xi-tu-jie-63-bu-0qyz7/

Java 代码

    public int uniquePathsWithObstacles2(int[][] nums) {
        int n = nums.length,m = nums[0].length;
        int[] dp = new int[m];
        for(int i = 0; i < n; i++){
            for(int j = 0; j < m; j++){
                if(i == 0 && j == 0) dp[j] = 1; //初始条件
                if(nums[i][j] == 1){
                    dp[j] = 0;
                    continue;
                }
                if(j > 0) dp[j] = dp[j] + dp[j- 1];

            }
        }
        return dp[m-1];
    }