最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

本题的背景是一个造桥项目，初始给定我们 $n$ 座打算建造的桥

每座桥有两个参数 $x_1$ 和 $x_2$，表示该桥一头连接在上岸坐标为$x_1$的地方，一头连在下岸坐标为$x_2$的地方

题目要求我们找出一种建桥方案，使得在所有建造的桥不相交的前提下，建造尽可能多的桥

求出该方案的造桥数量

具体的情况用文字可能不太好解释，我这里画了一张图方便大家理解

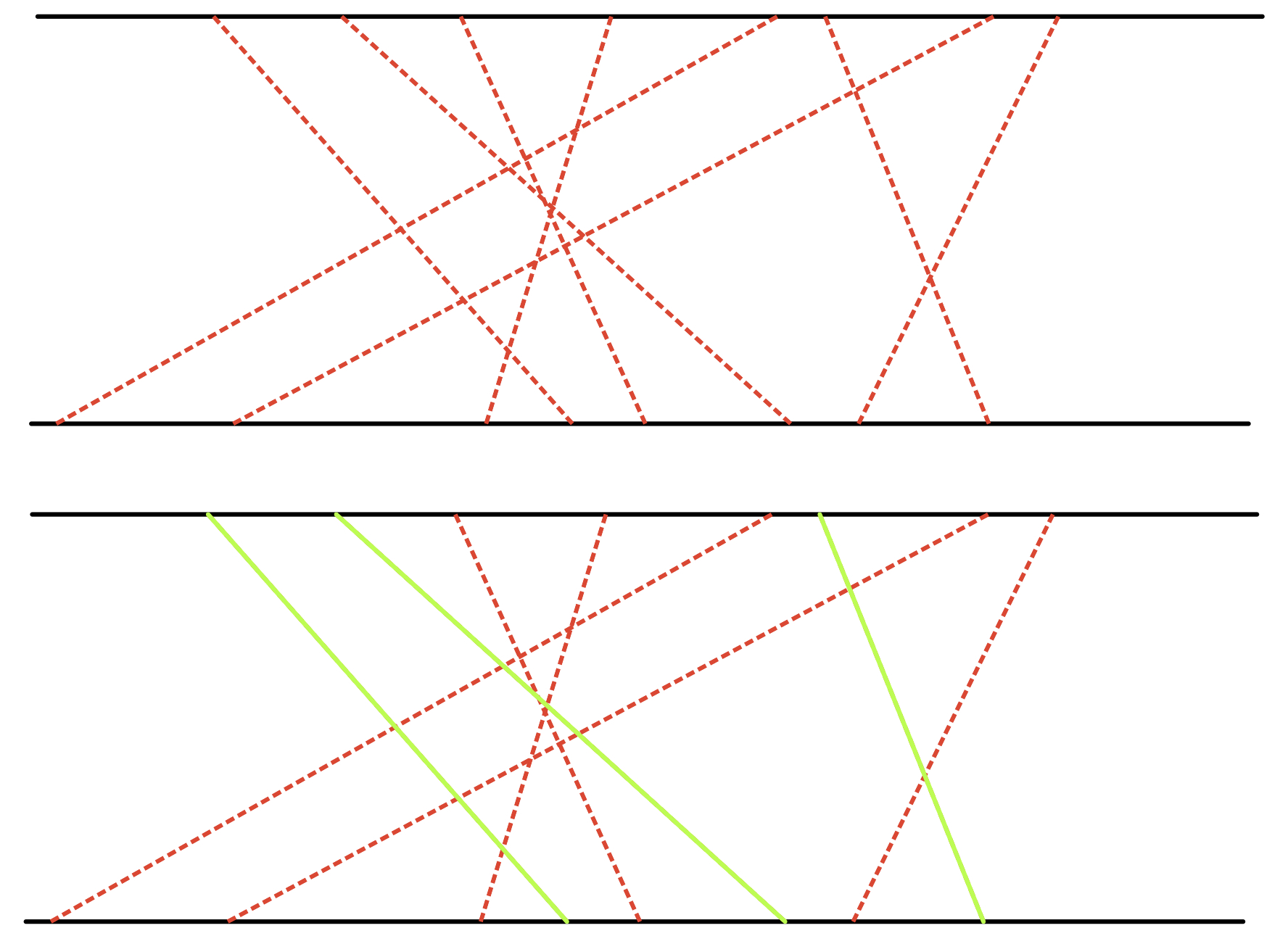
红色虚线表示初始提供的打算建造的桥

我们要找出的方案是在不相交的前提下的最大建桥数量

也就是上面的绿线连接而成的方案

这就是本题的大致意思

题解

我们先想一下暴力怎么做

很容易想到，我们可以枚举所有的方案，然后检查方案是否合法，如果合法就考虑是否能够更新最大值答案

这么做的时间复杂度是 $O(2^n)$，而 $n$ 的数据范围是 $5000$，毫无疑问会超时。

所以，我们就需要找出一些性质进行优化

既然是要暴力枚举，我们可以考虑一个枚举方案，按照上岸的坐标从小到大来枚举

然后我们只需关心下岸的坐标之间有何关系即可

于是，可以轻易发现，上坐标从小到大枚举选择到的桥，其对应下坐标也必然是从小到大的

具体见下图：

蓝色表示该方案按照上坐标从小到大先选出来的桥

红色表示该方案的下一座桥的下坐标不是从小到大的，绿色表示是从小到大的

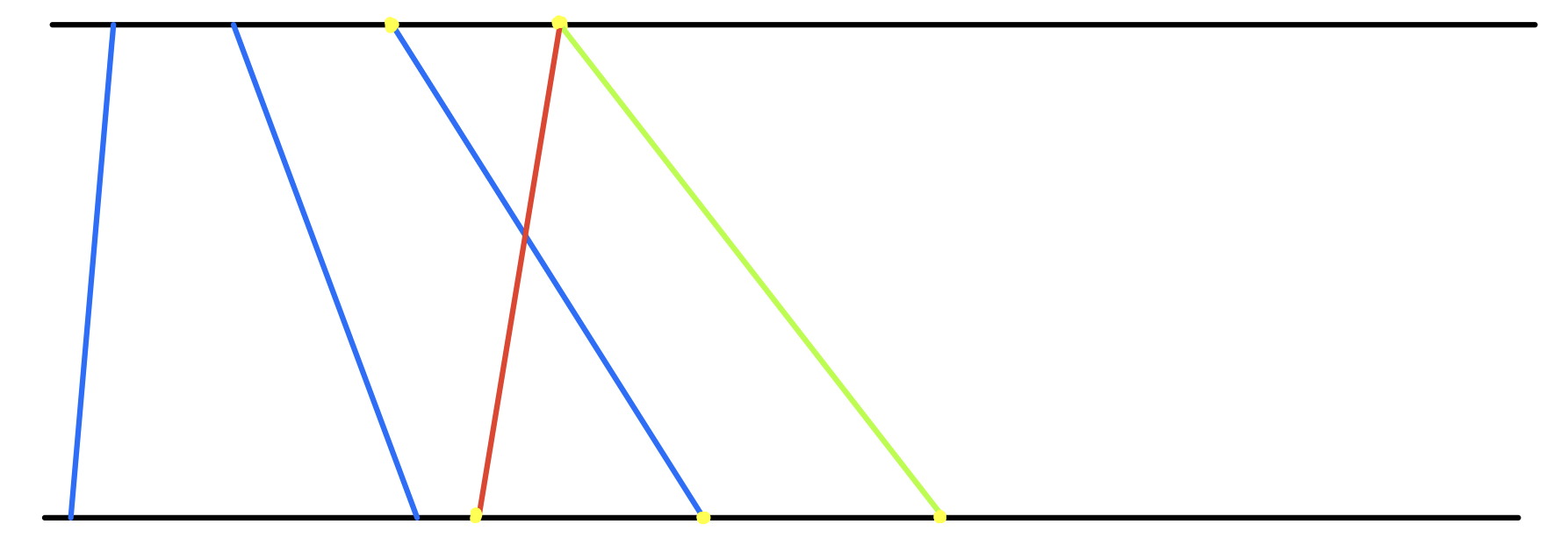
因此，该方案中，在上坐标排序的情况下，下坐标次序不是从小到大的，则必然不合法（会有相交）

于是，这题就变成了：桥以上坐标从小到大排序后，找出下坐标的最长上升子序列长度

关于如何求最长上升子序列模型的DP，大家可以看一下之前的博客，里面有详细的闫氏DP分析法

Code

我们可以用pair或者struct先把所有的桥存下来，然后按照上坐标排序

再然后，下坐标就构成了一个序列，我们只需找出该序列的最长上升子序列的长度，就求出本题的答案了

#include <iostream>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int,int> PII;

const int N = 50010;

int n;
int f[N];
PII p[N];

int main()
{
    //input
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> p[i].x >> p[i].y;
    //sort
    sort(p + 1, p + n + 1);
    //dp
    for (int i = 1; i <= n; ++ i)
    {
        for (int j = 0; j < i; ++ j)
        {
            if (p[j].y < p[i].y) f[i] = max(f[i], f[j] + 1);
        }
    }
    //find result
    int res = 0;
    for (int i = 1; i <= n; ++ i) res = max(res, f[i]);
    //output
    cout << res << endl;
    return 0;
}