题目描述
在给定的 N 个整数 A1,A2……AN 中选出两个进行 xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数 N。
第二行输入 N 个整数 A1~AN。
输出格式
输出一个整数表示答案。
数据范围
1≤N≤1e5,
0≤Ai<231
输入样例:
3
1 2 3
输出样例:
3
由数据范围反推算法复杂度以及算法内容
一般ACM或者笔试题的时间限制是1秒或2秒。
在这种情况下,C++代码中的操作次数控制在1e7∼1e8 为最佳。
下面给出在不同数据范围下,代码的时间复杂度和算法该如何选择:
1、n≤30, 指数级别, dfs+剪枝,状态压缩dp
2、n≤100 => O(n3),floyd,dp,高斯消元
3、n≤1000 => O(n2),O(n2logn),dp,二分,朴素版Dijkstra、朴素版Prim、Bellman-Ford
4、n≤10000 => O(n∗√n),块状链表、分块、莫队
5、n≤100000 => O(nlogn) =>各种sort,线段树、树状数组、set/map、heap、拓扑排序、
dijkstra+heap、prim+heap、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分
6、n≤1000000 => O(n), 以及常数较小的(nlogn) 算法 => 单调队列、hash、双指针扫描、并查集,kmp、AC自动机;
常数比较小的 O(nlogn)的做法:sort、树状数组、heap、dijkstra、spfa
7、n≤10000000 => O(n),双指针扫描、kmp、AC自动机、线性筛素数
8、n≤1e9 => O(√n),判断质数
9、n≤1e18 => O(logn),最大公约数,快速幂
10、n≤1e1000 => O((logn)²),高精度加减乘除
11、n≤1e100000 => O(logk×loglogk),k表示位数O(logk×loglogk),k表示位数,高精度加减、FFT/NTT
算法1(朴素TLE)
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10;
int a[N];
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++) scanf("%d",&a[i]);
int res=0;
for(int i=0;i<n;i++)
for(int j=0;j<n;j++)
res=max(res,a[i]^a[j]);
printf("%d",res);
return 0;
}
算法2
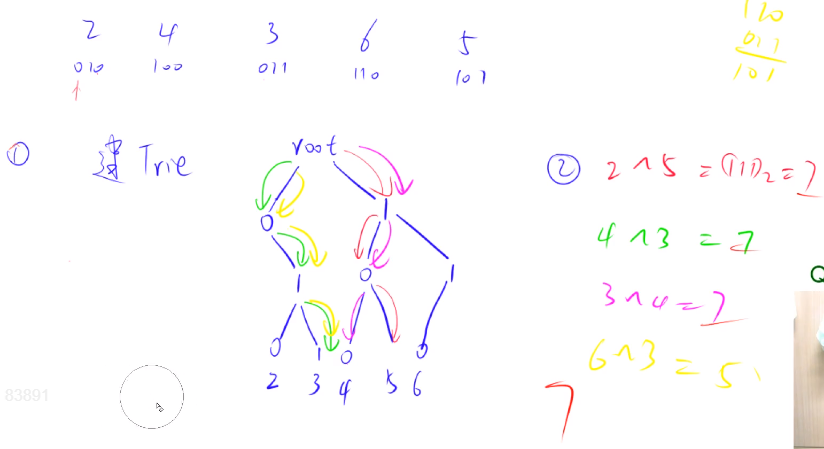
#include<iostream>
#include<algorithm>
using namespace std;
const int N=100010,M=31*N;
int idx,n,a[N];
int son[M][2];
void insert(int x)
{
int p=0;
for(int i=30;~i;i--)
{
int u=x>>i&1;
if(!son[p][u])
{
son[p][u]=++idx;
}
// else
// {
p=son[p][u];
// }
}
}
int query(int x) //query得到的是与x异或之后的值最大的已存在的a[i]中的数,即整个路径上所表示的数
{
int p=0,res=0;
for(int i=30;~i;i--)
{
int u=x>>i&1;
if(son[p][!u])
{
res=res*2+!u;
p=son[p][!u];
}
else
{
res=res*2+u;
p=son[p][u];
}
}
return res;
}
int main()
{
scanf("%d",&n);
int res=0;
for(int i=0;i<n;i++) scanf("%d",&a[i]);
for(int i=0;i<n;i++)
{
insert(a[i]);
int t=query(a[i]);
res=max(res,a[i]^t); //a[i]^t是二者异或之后的最大值
}
printf("%d",res);
return 0;
}
算法3
#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e5+10,M=3e6;//M=31*N
int a[N];
int son[M][2];//第二维度:只有两种状态0 or 1;
//而第一维的大小是二进制表示下一共有多少位数,数字一共有N个,N是小于1e5的,一个数在int下是32位,
// 又因为本题的题目范围是0≤Ai<2的31,所以每个数都是31位长度的二进制(或者说第32位都是0,不必再看),所以最高位是第30位,则我们需要最多3100000的一维坐标
int idx;
void insert(int x) //1:建Trie
{
int p=0;
for(int i=30;~i;i--)//本题数据<2的31,所以最高位是第30位,最低位是第0位,又因为求最大值,所以要优先保证较高位的值与所查不同(异或结果为1,数值越大),故i从30->0
{
int &s=son[p][x>>i&1];//&s是因为s的值需要被修改,加上引用符号之后,s的值改变时,son[][]的值也会随之改变。
if(!s) s=++idx;//若该孩子未存在,则创建
p=s;//存在则移至下一孩子节点
}
}
int query(int x) //2:枚举每个数
{
int res=0,p=0;//当前指针
for(int i=30;~i;i--)//~i意即i>=0,因为i=-1时,-1=(11111...1),~(-1)=0
{
int s=x>>i&1;//看一下x的二进制的第i位(从最高位依次取起)上是0还是1
if(son[p][!s])//若下一孩子节点存在与s相异的点
{
res+=(1<<i);//结果值的当前位异或结果为1,将其设置为1即可 //因为<<的优先级大于+=,所以括号可省略,即:res+=1<<i;
p=son[p][!s];//则移至相异孩子节点
}
else p=son[p][s];//若下一孩子节点不存在与s相异的点,则走与s相同的点
}
return res;//直接返回异或之后的最大值
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&a[i]);
insert(a[i]);
}
int res=0;
for(int i=0;i<n;i++)
{
res=max(res,query(a[i]));
}
printf("%d",res);
return 0;
}
算法4
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
/**
* Created by Yolanda on 2021/6/1 21:29
*/
public class Main {
private static final int M=3000000;
private static final int[][] son =new int[M][2];
private static int idx;
static void insert(int x)
{
int p=0;
for(int i=30;i>=0;i--)
{
// int s=son[p][(x>>i)&1];//此处不能这样写,C++中是int &s,后面当s值改变时,son会随之改变,这里则不能,所以要整体写
if(son[p][(x>>i)&1]==0) son[p][(x>>i)&1]=++idx;
p=son[p][(x>>i)&1];
}
}
static int query(int x)
{
int res=0,p=0;
for(int i=30;i>=0;i--)
{
int s=(x>>i)&1;
if(son[p][1-s]!=0)
{
res+=(1<<i);
p=son[p][1-s];//C++的!s,此处写为1-s
}
else
{
p=son[p][s];
}
}
return res;
}
public static void main(String[] args) throws IOException {
int res=0;
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
int n=Integer.parseInt(br.readLine());
int[] a=new int[n];//切勿多开,多开未赋值者为0,此处求max虽不影响结果,但若求min会有影响!
String[] s=br.readLine().split(" ");
for(int i=0;i<n;i++)
{
a[i]=Integer.parseInt(s[i]);
insert(a[i]);
}
for(int num:a)
{
res=Math.max(res,query(num));
}
System.out.println(res);
}
}

