题目描述

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

样例

输入：nums = [-2,1,-3,4,-1,2,1,-5,4]
输出：6
解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

输入：nums = [1]
输出：1

输入：nums = [0]
输出：0

输入：nums = [-1]
输出：-1

输入：nums = [-100000]
输出：-100000

算法1

(暴力枚举) $O(n^2)$

思路: 因为题目要求的答案是连续的子数组的和,那么得到的答案必然相邻之间的数相加得出来的,所以以当前i 为起点,枚举到nums[nums.length - 1] 的各种组合的和,从中记录最大值,枚举完以后返回这个值.

时间复杂度

O(n^2)

参考文献

Java 代码

public class 最大子序和 {
    //暴力搜索
    public int maxSubArray(int[] nums) {
        int res = Integer.MIN_VALUE;
        for(int i = 0; i < nums.length; i++){
            int temp = 0;
            for(int j = i; j < nums.length; j++){
                temp += nums[j];
                res = Math.max(res,temp);
            }
        }
        return res;
    }

}

算法2

(动态规划) $O(n)$

因为暴力枚举非常耗费时间,所以我们得想办法对它进行优化.那怎么进行优化呢?
我们其实是没有必然对所有的子数组的和进行枚举计算的,我们可以用一个数(可以成为标志位或者变量或者状态位)来代表一类数。什么意思? 比如我们在暴力枚举得到的结果是什么？ 就是每一次枚举每一个nums[i] 时,从[i,nums.length-1] 这个区间中的最大和,然后记录到一个变量res中,然后继续nums[i+1] 的枚举,接着和res 的数进行比较.

那我们就可以把这个核心思想给抽出来: 每次枚举num[i] 时,记录[0,i]的最大和.
那动态规划的样貌就出来了:用一个数去代表一类数的属性结果.

来自y 总的动归思路图:

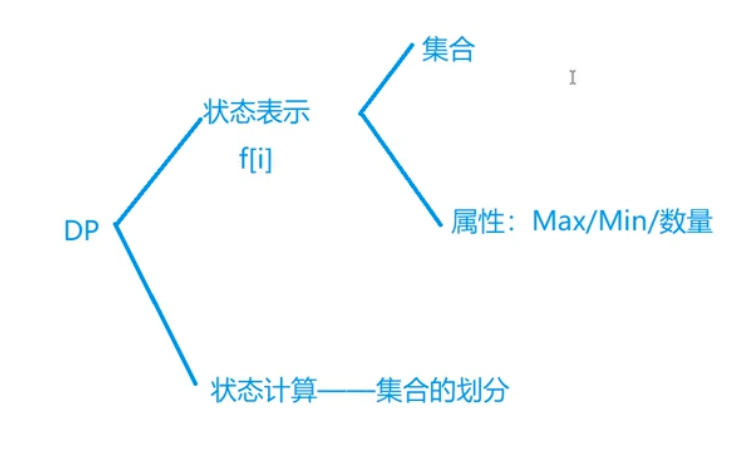
状态表示: dpi,它所表示的集合的为: 从[0,i] 区间内的组合; 属性为所有组合的的最大值. 所以dp[i] = [0,i] 区间内的所有组合的最大值.

状态计算:因为题目要求的是计算出连续子数组的最大和,所以dp[i] = dp[i-1] + nums[i],但是计算的是最大和,所以计算过程有两种情况: 1.dp[i-1] < 0 , dp[i] = nums[i]. 2.dp[i-1] >=0 ,dp[i] = dp[i-1] + nums[i]

初始条件: dp[0] = nums[0],表示从[0,0] 的区间内最大和为nums[0].

时间复杂度

O(n)

参考文献

https://www.bilibili.com/video/BV15441117yb

Java 代码

class Solution {
    public int maxSubArray(int[] nums) {
        int[] dp = new int[nums.length];
        dp[0] = nums[0];
        int res = nums[0];
        for(int i = 1; i < nums.length; i++){
            dp[i] = Math.max(dp[i-1],0) + nums[i];
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}