最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

题目给定一个长度为 $n$ 的数组 $a[n]$，表示某个景点的海拔高度

观光队从起点出发，初始海拔高度为 $0$，先上山后下山，且开始下山后不再往上走

让我们找出一个方案，使得观光队浏览到的景点数量最多

题解

此题和上题 AcWing 1017. 怪盗基德的滑翔翼 有着异曲同工之妙

上题求的是从一个点开始，朝向一个方向求一个最长下降子序列

本题则是让我们求一个先上升后下降的最长子序列，具体如下图所示

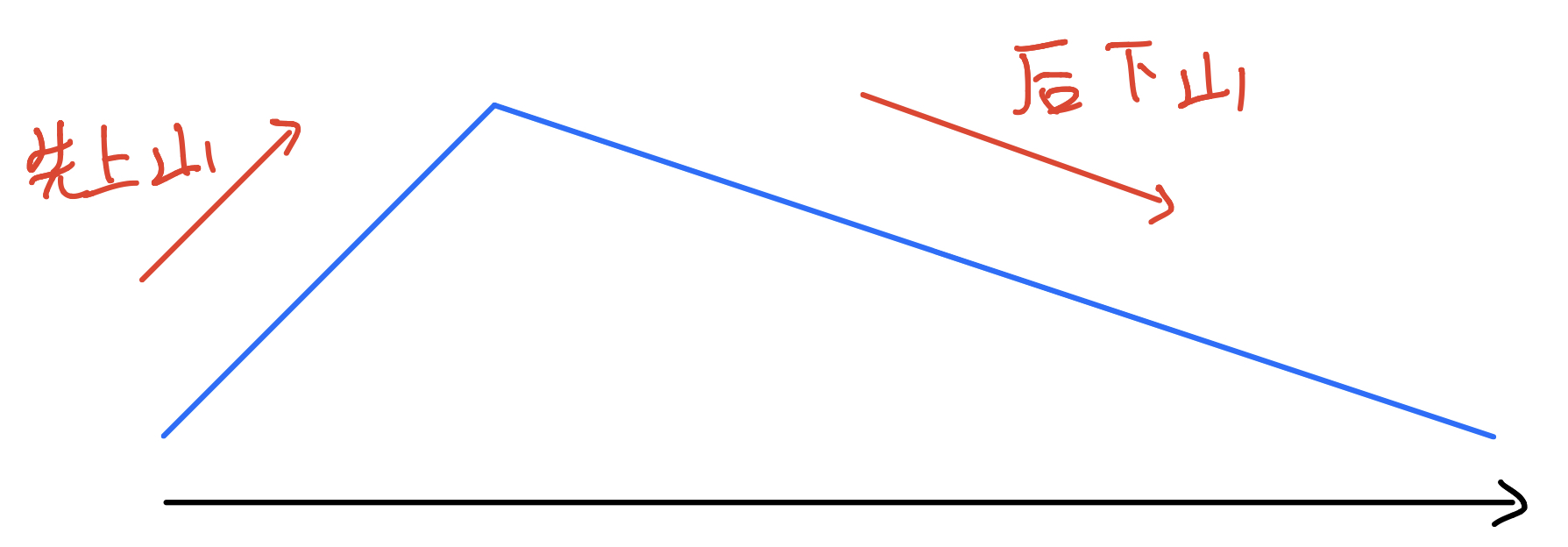
当然也和上题一样存在边界情况，即最优解答案可以是一个单调下降子序列或单调上升子序列

这种边界情况一样是先上升后下降的最长子序列的子集，因此不用额外讨论

一种做法是和上题一样，先做一遍最长上升，再做一遍最长下降

然后根据状态表示的特性，将两个状态的值相加，取一个 $\mathrm{Max}$ 就是 先上升后下降的最长子序列的长度

具体代码，以及DP模型的详细分析，参照这篇博客即可 AcWing 1017. 怪盗基德的滑翔翼

我这里给一个不同的思路

这是我做过 AcWing第二场热身赛的C题——AcWing 3549. 最长非递减子序列 后总结出来的一类模型

那就是，利用状态机模型DP解决最长xxx子序列模型的方法

xxx可以是先上升后下降，或者先上升后下降再上升，或者先上升后下降再上升再下降 ···

回到本题，我们就可以先利用状态机模型进行分析，具体如下：

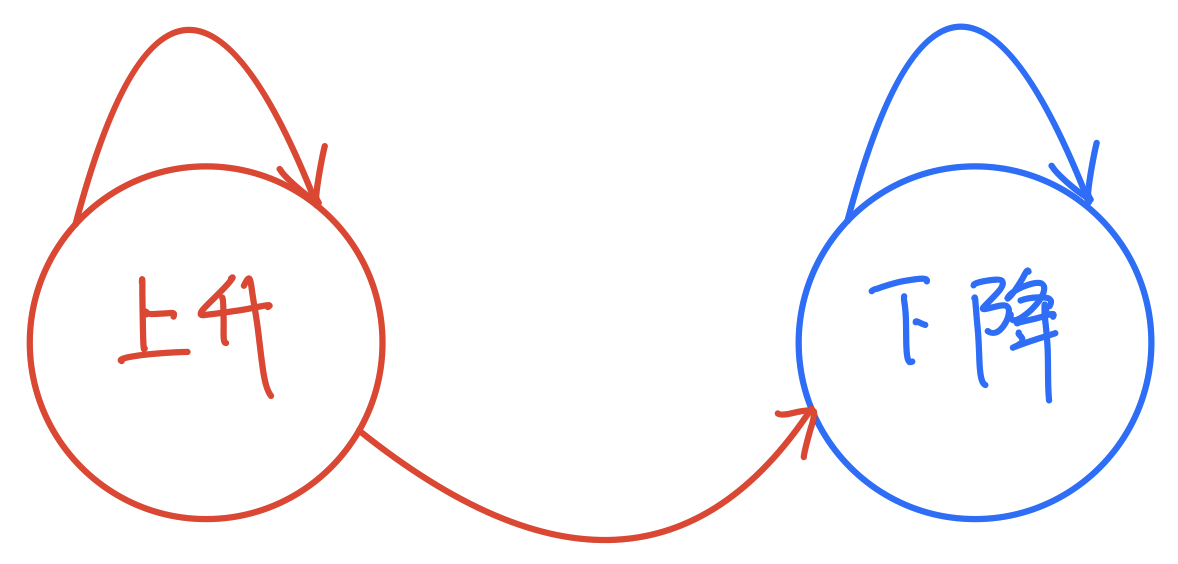
对于本题来说，当前状态如果是上升状态，则他下一个阶段可以维持上升状态，或者变成下降状态

而对于已经处于下降状态来说的状态，下一个阶段只能继续维持下降状态

于是我们便可以写出状态机模型的闫氏DP分析法：

闫氏DP分析法

$$ \begin{cases} 状态表示f_{i,j} \begin{cases} 集合: 以第i个位置作为当前子序列的右端点，且当前状态为j \\\ 属性: 方案的子序列长度最大 Max \end{cases} \\\ 状态转移 \begin{cases} f_{i,0} = max\{\sum f_{k,0}\}+1 \\\ f_{i,1} = max\{\sum f_{k,0}, \sum f_{k,1}\} + 1 \end{cases} \end{cases} $$

初始状态: f[0][0]和f[0][1]

目标状态: f[i][0]和f[i][1]

大家想更近一步了解这类模型的话，可以做一下这道题 AcWing 3549. 最长非递减子序列

Code

#include <iostream>

using namespace std;

const int N = 1010;

int n;
int a[N];
int f[N][2];

int main()
{
    //input
    cin >> n;
    for (int i = 1; i <= n; ++ i) cin >> a[i];

    //dp
    for (int i = 1; i <= n; ++ i)
    {
        f[i][0] = f[i][1] = 1;
        for (int k = 1; k < i; ++ k)
        {
            if (a[k] < a[i]) f[i][0] = max(f[i][0], f[k][0] + 1);
            if (a[k] > a[i]) f[i][1] = max(f[i][1], max(f[k][0], f[k][1]) + 1);
        }
    }

    //find result from all final states
    int res = 0;
    for (int i = 1; i <= n; ++ i) res = max(res, max(f[i][0], f[i][1]));
    cout << res << endl;

    return 0;
}