题目描述

给你一个 m x n 的整数矩阵 grid。

菱形和 指的是 grid 中一个正菱形 边界 上的元素之和。本题中的菱形必须为正方形旋转 45 度，且四个角都在一个格子当中。下图是四个可行的菱形，每个菱形和应该包含的格子都用了相应颜色标注在图中。

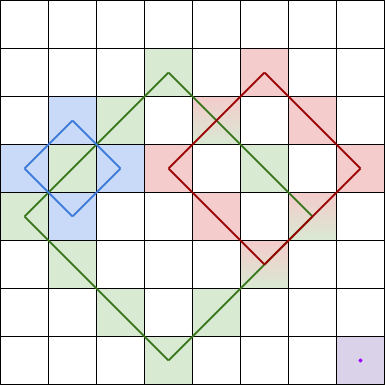
注意，菱形可以是一个面积为 0 的区域，如上图中右下角的紫色菱形所示。

请你按照 降序 返回 grid 中三个最大的 互不相同的菱形和。如果不同的和少于三个，则将它们全部返回。

样例

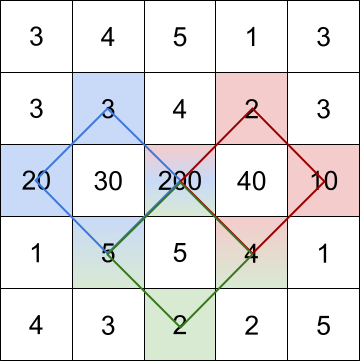
输入：grid = [[3,4,5,1,3],[3,3,4,2,3],[20,30,200,40,10],[1,5,5,4,1],[4,3,2,2,5]]
输出：[228,216,211]
解释：最大的三个菱形和如上图所示。
- 蓝色：20 + 3 + 200 + 5 = 228
- 红色：200 + 2 + 10 + 4 = 216
- 绿色：5 + 200 + 4 + 2 = 211

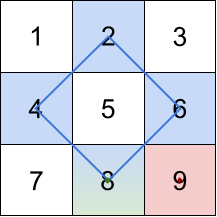
输入：grid = [[1,2,3],[4,5,6],[7,8,9]]
输出：[20,9,8]
解释：最大的三个菱形和如上图所示。
- 蓝色：4 + 2 + 6 + 8 = 20
- 红色：9 （右下角红色的面积为 0 的菱形）
- 绿色：8 （下方中央面积为 0 的菱形）

输入：grid = [[7,7,7]]
输出：[7]
解释：所有三个可能的菱形和都相同，所以返回 [7]。

限制

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• 1 <= grid[i][j] <= 10^5

算法

(暴力枚举) $O(mn\min(m, n))$

1. 初始化每个对角线和每个反对角线的前缀和。
2. 枚举菱形的边长，最小为 1，最大为 $(\min(n, m) + 1) / 2$。边长为 1 时相当于面积为 0。
3. 对于每种边长，枚举菱形的中心点，并通过预处理的前缀和求出周长。注意，当面积为 0 时，周长需要特殊处理。
4. 使用哈希表判断数字是否出现过，并使用一个容量为 3 的小根堆记录周长最大的三个菱形。

时间复杂度

• 预处理需要 $O(mn)$ 的时间。
• 共有 $O(\min(m, n))$ 种菱形，每种有 $O(mn)$ 个菱形，仅需要常数的时间求一个菱形的周长。
• 故总时间复杂度为 $O(mn\min(m, n))$。

空间复杂度

• 需要 $O(mn)$ 的额外空间存储前缀和数组以及哈希表。

C++ 代码

class Solution {
public:
    vector<int> getBiggestThree(vector<vector<int>>& grid) {
        const int m = grid.size(), n = grid[0].size();

        vector<vector<int>> sum1(m, vector<int>(n)), sum2(m, vector<int>(n));

        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++) {
                if (i == 0 || j == 0) sum1[i][j] = grid[i][j];
                else sum1[i][j] = sum1[i - 1][j - 1] + grid[i][j];
            }

        for (int i = 0; i < m; i++)
            for (int j = n - 1; j >= 0; j--) {
                if (i == 0 || j == n - 1) sum2[i][j] = grid[i][j];
                else sum2[i][j] = sum2[i - 1][j + 1] + grid[i][j];
            }

        unordered_set<int> seen;

        priority_queue<int, vector<int>, greater<int>> heap;

        for (int len = 1; len <= (min(m, n) + 1) / 2; len++)
            for (int i = len - 1; i + len - 1 < m; i++)
                for (int j = len - 1; j + len - 1 < n; j++) {
                    int up = i - len + 1;
                    int left = j - len + 1;
                    int down = i + len - 1;
                    int right = j + len - 1;

                    int sum = 0;
                    if (len > 1) {
                        if (up == 0 || j == n - 1) sum += sum2[i][left];
                        else sum += sum2[i][left] - sum2[up - 1][j + 1];

                        if (i == 0 || left == 0) sum += sum1[down][j];
                        else sum += sum1[down][j] - sum1[i - 1][left - 1];

                        if (i == 0 || right == n - 1) sum += sum2[down][j];
                        else sum += sum2[down][j] - sum2[i - 1][right + 1];

                        if (up == 0 || j == 0) sum += sum1[i][right];
                        else sum += sum1[i][right] - sum1[up - 1][j - 1];

                        sum -= grid[up][j] + grid[i][left] +
                            grid[down][j] + grid[i][right];
                    } else {
                        sum = grid[i][j];
                    }

                    if (seen.find(sum) != seen.end())
                        continue;


                    seen.insert(sum);
                    if (heap.size() < 3) {
                        heap.push(sum);
                    } else if (heap.top() < sum) {
                        heap.pop();
                        heap.push(sum);
                    }
                }

        vector<int> ans;
        while (!heap.empty()) {
            ans.push_back(heap.top());
            heap.pop();
        }

        reverse(ans.begin(), ans.end());
        return ans;
    }
};