A

取两个数组的最大值满足条件。

$\because A_i>0,B_i>0$

$\therefore \forall i,\max(A)+\max(B)>\max(A)\ge A_i$

$\max(A)+\max(B)\notin A$

同理可证：$\max(A)+\max(B)\notin B$

B

排序后二分最大中位数的值 $v$。

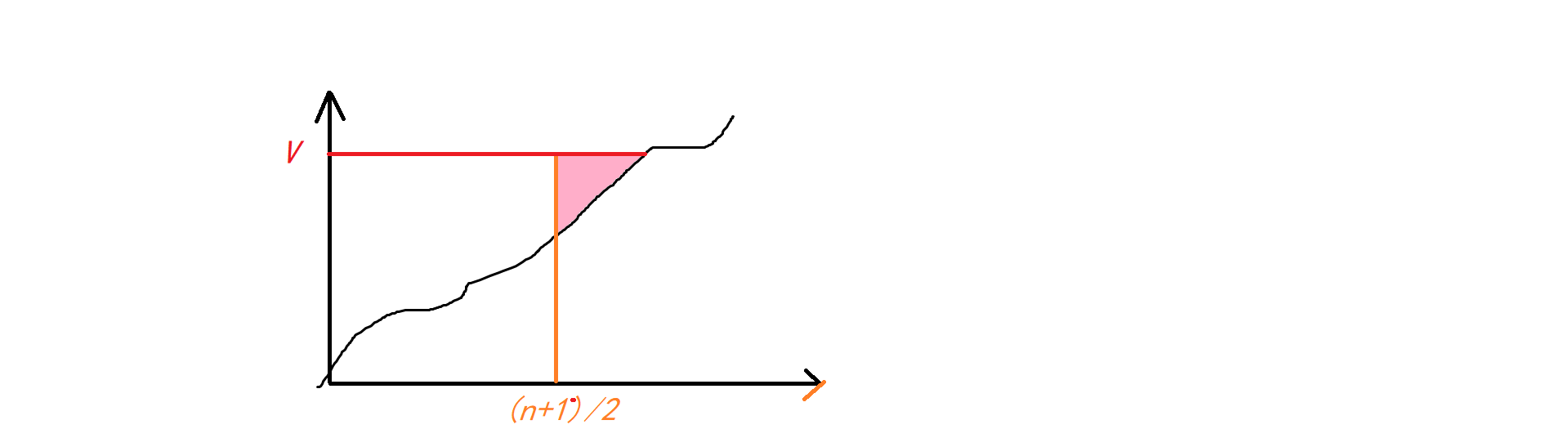
比较粉色区域补齐后所需的操作与 $k$ 的大小。

你可以直接扫一遍数组算，但我们有优化。

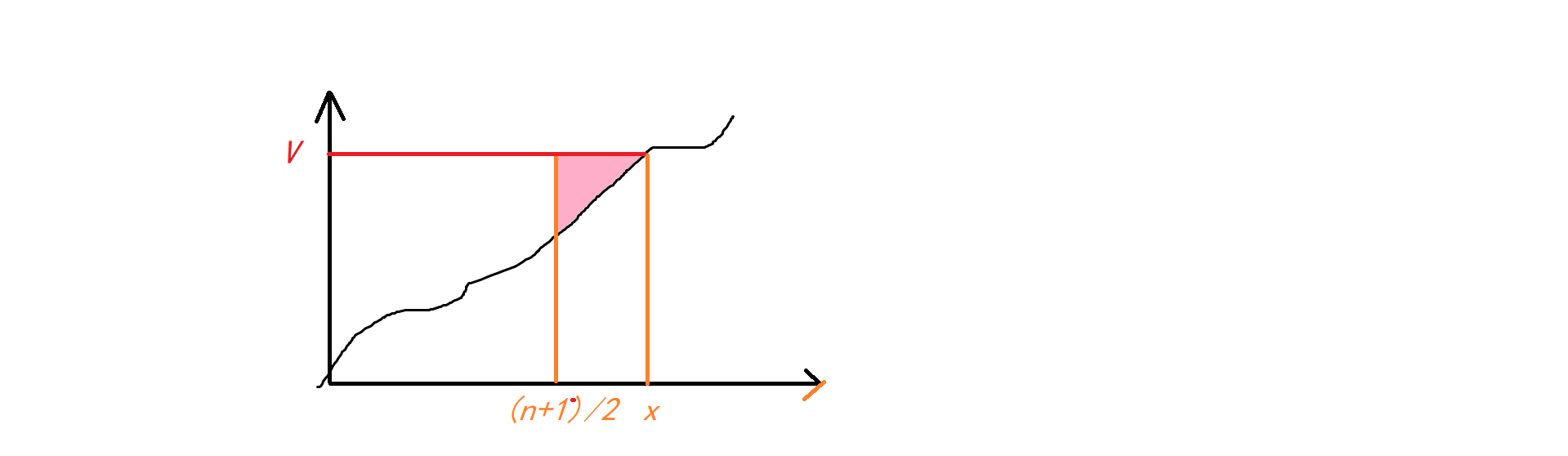
再用二分查出图中 $x$ 所在位置。粉色区域就是 $v(x-\frac{n+1}2+1)-\sum\limits_{i\in[\frac{n+1}2,x]}a_i$。

和式用前缀和维护，二分用upper_bound。

现在时间复杂度还是 $O(N\log N)$。但是效率会更高。

使用基数排序使得时间复杂度理论为：$O(\log SIZE\ \log N+N)$

C

我们把 $i$ 与 $p_i$ 连边。会形成一个内向基环树森林。

数据保证这张图退化成一个个环。

所以我们用并查集维护， $i$ 所在连通块大小就是答案。

时间复杂度 $O(n\alpha(n))$