分析

• 本题的考点：并查集。

• 根据容斥原理，本题一定存在答案。观察可知，本题相当于求环的长度，可以直接求，也可以使用并查集。

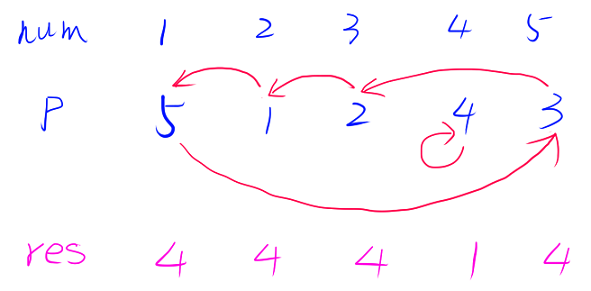
代码

• C++

#include <iostream>
#include <cstring>

using namespace std;

const int N = 200010;

int n;
int p[N], res[N];
bool st[N];  // 记录数字i是否已经得到结果

int main() {

    int T;
    scanf("%d", &T);
    while (T--) {
        scanf("%d", &n);
        for (int i = 1; i <= n; i++) scanf("%d", &p[i]);

        memset(st, 0, sizeof st);
        for (int i = 1; i <= n; i++)
            if (!st[i]) {
                int j = i, s = 1;  // s表示整个环上的边数
                for (; p[j] != i; j = p[j]) s++;
                do {
                    st[j] = true;
                    res[j] = s;
                    j = p[j];
                } while (p[j] != i);
            }
        for (int i = 1; i <= n; i++) printf("%d ", res[i]);
        puts("");
    }

    return 0;
}

时空复杂度分析

• 时间复杂度：$O(n \times T)$，n为数组的长度，T为组数。

• 空间复杂度：$O(n)$。