分析

• 本题的考点：数学。

• 假设数据元素有n个。

• 步骤如下：

（1）首先将数组按升序排序；

（2）然后从中位数开始向后遍历，每次找到一段连续的且数值相等的最长的数据，假设对应区间为[n / 2, j)，该区间一共有cnt = j-n/2个数，如果要让中位数变大的话，这cnt个数都必须增加相同的数。

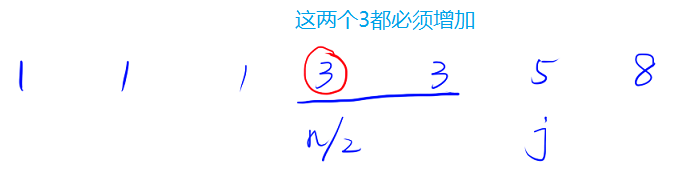
• 需要考虑一些细节：每次这cnt最大可以增加到多少，只有k>=cnt时，这些数才能同时增加，具体增加多少需要需要分情况讨论：

（1）当j < n时，说明后面还存在数据，且nums[j] != nums[j - 1]，最大增大的数为min(k / cnt, a[j] - a[i])；

（2）否则的话，说明我们已经考察完整个数组了，最大增大的数为k /= cnt；

代码

• C++

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 200010;

int n, k;
int a[N];

int main() {

    cin >> n >> k;
    for (int i = 0; i < n; i++) scanf("%d", &a[i]);

    sort(a, a + n);
    int up = 0;  // 中位数可以增加多大
    for (int i = n / 2, cnt = 0; i < n; i++) {  // cnt表示一共需要增加几个数
        int j = i;
        while (j < n && a[j] == a[i]) j++;
        cnt += j - i;
        if (k >= cnt) {
            if (j < n) {
                int t = min(k / cnt, a[j] - a[i]);  // t为最大可以增大多少
                k -= t * cnt;
                up += t;
            } else {
                int t = k /= cnt;
                k -= t * cnt;
                up += t;
            }
        } else break;
        i = j - 1;
    }
    printf("%d\n", a[n / 2] + up);

    return 0;
}

时空复杂度分析

• 时间复杂度：$O(n \times log(n))$，n为数组的长度。

• 空间复杂度：$O(n)$。