最近在补全提高课所有题目的题解，宣传一下汇总的地方提高课题解补全计划

题目描述

题目开始给定一个下标从 $1$ 开始，长度为 $n$ 的数组，即 $\{1,2,\cdots,n\}$

再给定每个下标每轮移动到的新的下标的数组 $p[n]$

上面的话翻译一下就是：下标为 $i$ 的元素进行一轮移动会到 $p[i]$ 的下标上

问每个数字经过多少次变换，会回到原来的位置上。

解析

这类数字坐标移动是个比较经典的图论模型

我拿测试样例建个图，具体如下：

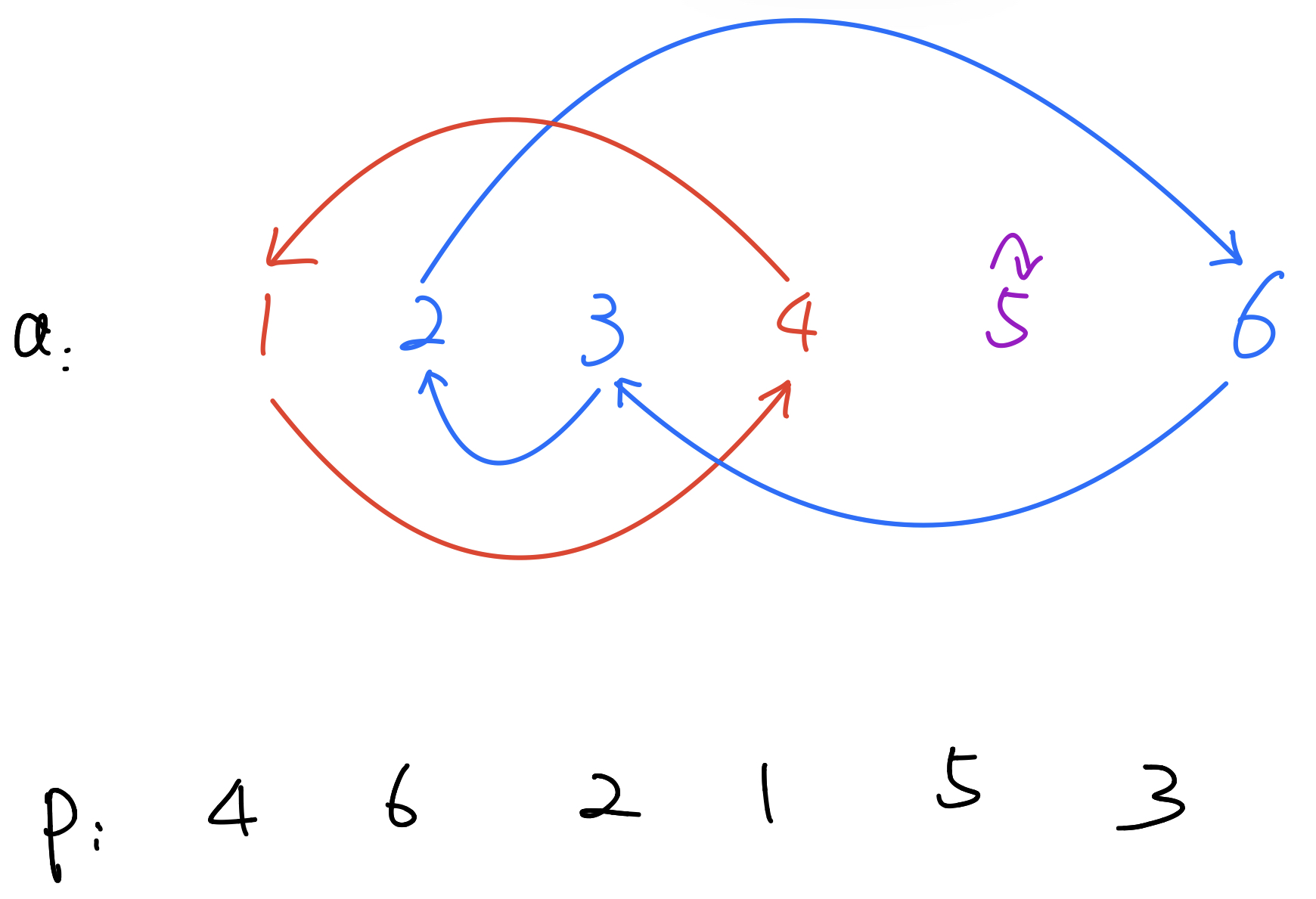
因为每个点的出度和入度都为 $1$，所以每组交换都会形成一个闭环

对应每个环中的节点个数 $t$，就是每个元素最终回到自己原来位置时需要的经过的交换轮数 $t$

那么本题就是求每个元素对应环中的节点个数

我们可以采用并查集维护各个连通块（环）的连通性，然后在并查集的头节点额外维护该并查集的节点个数即可

类似的图论模型还有经过多少次操作可以把每个连通块变成自环（容我找一下，等下上链接）

Code

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 2e5 + 10;

int T, n;
int a[N], p[N], s[N];

int find(int x)  // 并查集
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    scanf("%d", &T);
    while (T -- )
    {
        scanf("%d", &n);
        for (int i = 1; i <= n; i ++ ) p[i] = i, s[i] = 1;
        for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);

        for (int i = 1; i <= n; i ++ )
        {
            if (a[i] != i)
            {
                int pa = find(i), pb = find(a[i]);
                if (pa != pb)
                {
                    s[pb] += s[pa];
                    p[pa] = pb;
                }
            }
        }
        for (int i = 1; i <= n; ++ i) cout << s[find(i)] << " ";
        cout << endl;
    }
    return 0;
}