Blog

题目

Luogu
LOJ
Acwing

思路

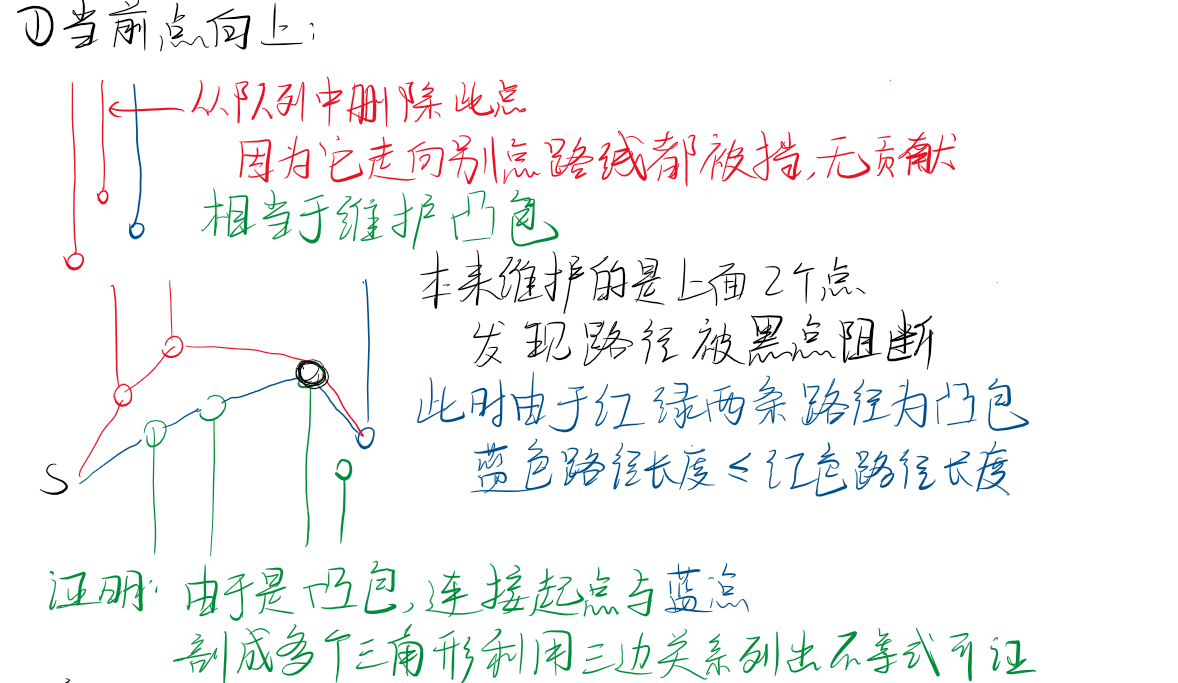
代码

#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 1e6 + 10;
struct PDD { double x, y; } S, T;
PDD operator-(PDD a, PDD b) { return (PDD){ a.x - b.x, a.y - b.y }; }
double operator*(PDD a, PDD b) { return a.x * b.x + a.y * b.y; }
double operator&(PDD a, PDD b) { return a.x * b.y - a.y * b.x;  }
// 直线起始点坐标以及朝上还是朝下, 朝上 1, 朝下 -1
struct LINE { PDD p; int dir; } L[N], A[N];
bool operator<(LINE a, LINE b) { return a.p.x < b.p.x; }
// 点积
double cro(PDD a, PDD b, PDD c) { return (b - a) & (c - a); }
double cro(int a, int b, int c) { return cro(L[a].p, L[b].p, L[c].p); }
double get_angle(PDD x) { return atan2(x.y, x.x); }
int n, hh[2], tt[2], q[2][N], pre[N];
int main() {
    S.x = S.y = 0;
    scanf("%d%lf%lf", &n, &T.x, &T.y);
    for (int i = 1; i <= n; i++) {
        double x, y, a;
        scanf("%lf%lf%lf", &x, &y, &a);
        PDD t = (PDD){ x, y };
        double l = get_angle(S - t), r = get_angle(T - t);
        // 判断一下这条线朝上还是朝下, 具体可以画图看
        if (l <= r && (a < r && a > l)) A[i] = (LINE){ t, -1 };
        else if (l <= r) A[i] = (LINE){ t, 1 };
        if (l >= r && (a > r && a < l)) A[i] = (LINE){ t, 1 };
        else if (l >= r) A[i] = (LINE){ t, -1 };
    }
    sort(A + 1, A + n + 1);
    // 筛选有用的点
    int cnt = 0;
    L[++cnt] = (LINE){ S, 1 };
    for (int i = 1; i <= n; i++) 
        if (A[i].p.x >= S.x && A[i].p.x <= T.x) 
            L[++cnt] = A[i];
    L[++cnt] = (LINE){ T, 1 };
    // 开始维护队列, 首先加入起点
    tt[0] = tt[1] = -1;
    q[0][++tt[0]] = q[1][++tt[1]] = 1;
    for (int i = 1; i <= cnt; i++) {
        int dir = L[i].dir, cur = (dir > 0) ? 0 : 1;
        // cout << cur << ' ' << dir << endl;
        // 0 系列表示当前点所在的队列, 1 表示对面的队列
        int &l0 = hh[cur], &r0 = tt[cur], *q0 = q[cur];
        int &l1 = hh[cur ^ 1], &r1 = tt[cur ^ 1], *q1 = q[cur ^ 1];
        // 当前队列至少有两个点, 队头绿点可以删
        if (l1 < r1 && cro(q1[l1], i, q1[l1 + 1]) * dir >= 0) {
            // 删掉可以删的绿点
            while (l1 < r1 && cro(q1[l1], i, q1[l1 + 1]) * dir >= 0) l1++;
            // 前置节点就是没被删的点, 同时创建虚拟上凸包
            pre[i] = q0[l0 = ++r0] = q1[l1];
        } else {
            while (l0 < r0 && cro(q0[r0 - 1], i, q0[r0]) * dir >= 0) r0--;
            pre[i] = q0[r0];
        }
        q0[++r0] = i;
    }
    double res = 0;
    for (int i = cnt; i > 1; i = pre[i])
        res += sqrt((L[i].p - L[pre[i]].p) * (L[i].p - L[pre[i]].p));
    printf("%.10lf", res);
    return 0;
}