「Floyd求最短路」题解

一.最短路的引入

最短路问题$（short-path problem）$是网络理论解决的典型问题之一，可用来解决管路铺设、线路安装、厂区布局和设备更新等实际问题。基本内容是：若网络中的每条边都有一个数值（长度、成本、时间等），则找出两节点（通常是源节点和阱节点）之间总权和最小的路径就是最短路问题。

$from$ 百度百科

说人话，就是一堆节点一堆路，每条路有一定的权值，求从指定起点到指定终点的最短长度。

有很多种常见算法，比如说 :

• $Dijkstra$
• $Floyd$
• $Bellman$
• $SPFA$
• $Johnson$
  …

其他算法以后会写，但这里只提到 $Floyd$ 最短路算法。

二.Floyd 算法

审题

比如说有一个图：

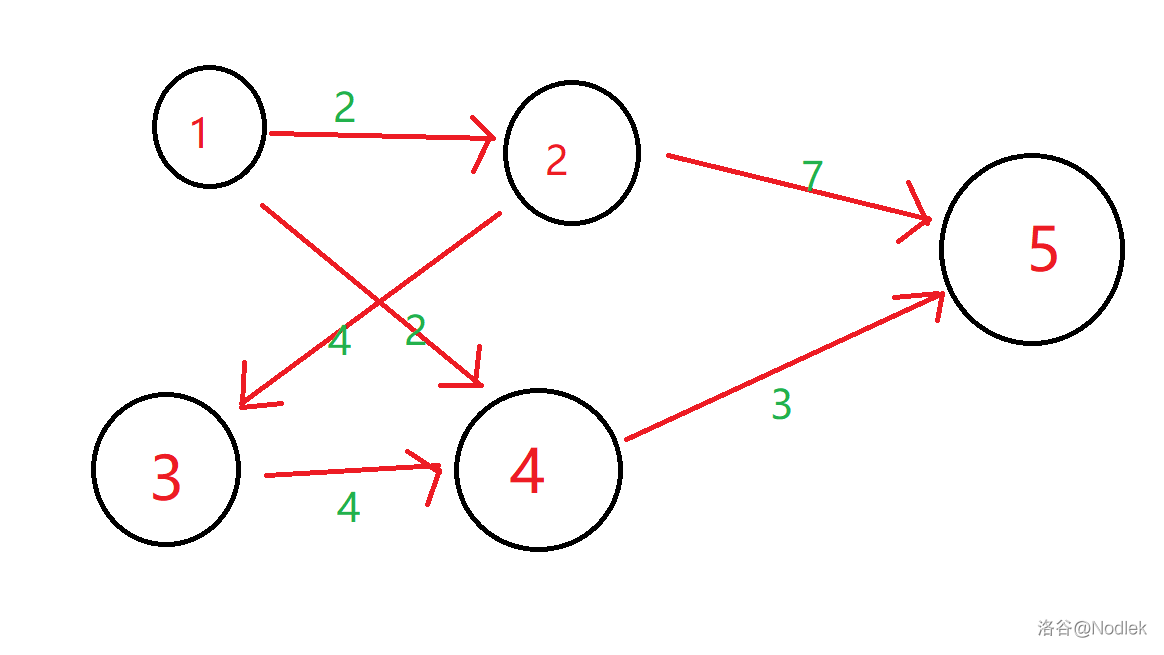
(图崩了，这里给出网址：https://cdn.luogu.com.cn/upload/image_hosting/0dljuq80.png)

假设求1->5的最短路。很容易就能看出来答案是 $5$ 。
那么我们怎么得出来答案 $5$ 的呢？
我们一步一步来：
贪心肯定不行，非常容易找到反例。
那怎么做呢？
众所周知，看起来像是贪心但是有反例的题，都可以用$DP$来做。

分析

那就来 $DP$ ！
定义：

$dp[i][j]:从节点i到节点j的最短路$

初始化：
易知， $dp[i][i]$ 一定为0，因为一个节点到自己的距离必为0；
$dp[i][j]\gets inf$ $(i \not= j)$

转移方程:
枚举两点的同时枚举中转点，考虑能否将两点距离缩到最小。
最后逐渐拓展到 $dp[1][5]$

$$e[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])$$

代码惊人的短，但是复杂度为 $O(n^3)$ ，惊人的高。
所以这里建议如果数据不超过1000时再考虑使用。

注意有重边，也就是说可能会得到多组起始点一样，但权值不一样的数据。求最短路故需要取最小值。

#include <iostream>
#include <algorithm>
using namespace std;
const int INF=(1<<29);
int e[205][205];
int n,m,k;
int main(void)
{
    cin>>n>>m>>k;
    for(register int i=1;i<=n;i++)
    {
        for(register int j=1;j<=n;j++)
        {
            if(i!=j)
            {
                e[i][j]=INF;
            }
        }
    }
    for(register int i=1;i<=m;i++)
    {
        int x,y,z;
        cin>>x>>y>>z;
        e[x][y]=min(e[x][y],z);
    }
    for(register int k=1;k<=n;k++)
        for(register int i=1;i<=n;i++)
            for(register int j=1;j<=n;j++)
                if(e[i][k]!=INF && e[k][j]!=INF)
                    e[i][j]=min(e[i][j],e[i][k]+e[k][j]);

    while(k--)
    {
        int x,y;
        cin>>x>>y;
        if(x==y)
        {
            printf("0\n");
            continue;
        }
        if(e[x][y]<INF)
        {
            cout<<e[x][y]<<endl;
            continue;
        }
        printf("impossible\n");
    }
}