高斯消元的本质就是化简成一个阶梯式的行列式。
首先线性方程组的解有以下三种情况：
+ 无解
+ 有无穷多个解
+ 有唯一解

高斯消元的步骤分为以下四步：
+ 枚举每一行找到当前行(包括当前行)下面的，当前列的绝对值最大的一个数。
+ 将其绝对值最大的一行移到上面
+ 将改行的第一个数变成1
+ 将下面所有的行的当前列都清成0

例子：

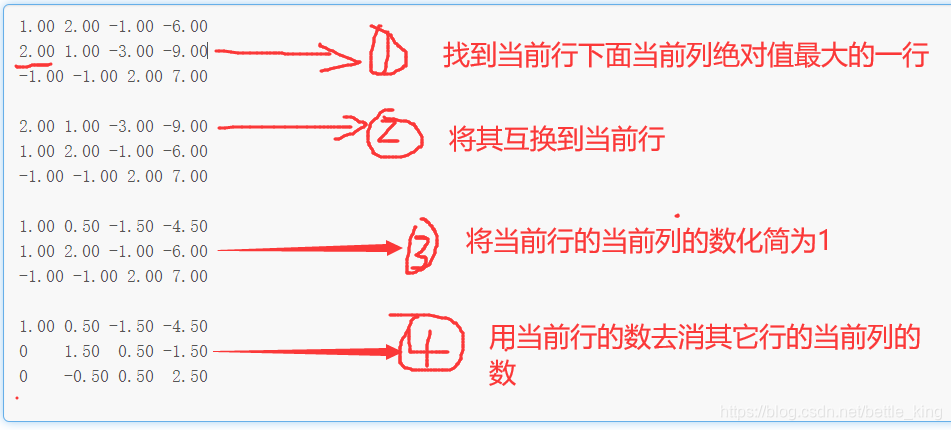
注意：这里刚开始是第一行和第一列，以此类推就会化简成一个阶梯行列式。

https://www.acwing.com/problem/content/description/885/
按照上面的步骤模拟的代码如下：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=110;
const double eps=1e-6;
double a[N][N];
int n;
void print()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n+1;j++)
        cout<<a[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
}
int gauss()
{
    int c,r;
    for(c=1,r=1;c<=n;c++)
    {
        int t=r;
        for(int i=r;i<=n;i++)//1 寻找 
        {
            if(fabs(a[i][c])>fabs(a[t][c])) t=i;
        }

        if(fabs(a[t][c])<eps) continue;

        for(int i=c;i<=n+1;i++) swap(a[r][i],a[t][i]);//2 交换

        for(int i=n+1;i>=c;i--) a[r][i]=a[r][i]/a[r][c];//3 化简 

        for(int i=r+1;i<=n;i++)//将该行下面的该列都清零
        {
            if (fabs(a[i][c]) > eps)//如果当前列不为0，为0的话就不用清了了。
            for(int j=n+1;j>=c;j--)
            {
                a[i][j]-=a[i][c]*a[r][j];
            }
        } 
        r++;
    }

    if (r <= n)//说明我们的 第r到 第n行都是全零。
    {
        for (int i = r; i <= n; i ++ )//如果常数项不为零就会产生  0 = 3  这种矛盾
            if (fabs(a[i][n+1]) > eps)
                return 2;//无解
        return 1;
    }

    for (int i = n; i >1 0; i -- )//倒着推解
        for (int j = i + 1; j <= n; j ++ )
            a[i][n+1] -= a[j][n+1] * a[i][j];

    return 0;
}
int main(void)
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n+1;j++)
        cin>>a[i][j];
    }
    int t=gauss();
    if (t == 0)
    {
        for (int i = 1; i <= n; i ++ ) printf("%.2lf\n", a[i][n+1]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");
    return 0;
}

下面开始回答一些常见的不懂的问题：

==问题一：为啥化简为 1的操作，和清零的操作都要倒着推。==


当然你也可以正着推，不过你要用一个变量来记录一下开头的元素的值。化简都除以这个值就行了。
不过着稍微有点麻烦。
那么此时的代码就如下所示：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N=110;
const double eps=1e-6;
double a[N][N];
int n;
void print()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n+1;j++)
        cout<<a[i][j]<<" ";
        cout<<endl;
    }
    cout<<endl;
}
int gauss()
{
    int c,r;
    for(c=1,r=1;c<=n;c++)
    {
        int t=r;
        for(int i=r;i<=n;i++)//1 寻找 
        {
            if(fabs(a[i][c])>fabs(a[t][c])) t=i;
        }

        if(fabs(a[t][c])<eps) continue;

        for(int i=c;i<=n+1;i++) swap(a[r][i],a[t][i]);//2 交换

        double x=a[r][c];
        for(int i=c;i<=n+1;i++) a[r][i]=a[r][i]/x;//3 化简 

        for(int i=r+1;i<=n;i++)
        {
            if (fabs(a[i][c]) > eps)
            {
                double x=a[i][c];
                for(int j=c;j<=n+1;j++)
                {
                    a[i][j]-=x*a[r][j];
                }
            }
        } 
        r++;
    }

    if (r <= n)
    {
        for (int i = r; i <= n; i ++ )
            if (fabs(a[i][n+1]) > eps)
                return 2;
        return 1;
    }

    for (int i = n; i >= 1; i -- )
        for (int j = i + 1; j <= n; j ++ )
            a[i][n+1] -= a[j][n+1] * a[i][j];

    return 0;
}
int main(void)
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n+1;j++)
        cin>>a[i][j];
    }
    int t=gauss();
    if (t == 0)
    {
        for (int i = 1; i <= n; i ++ ) printf("%.2lf\n", a[i][n+1]);
    }
    else if (t == 1) puts("Infinite group solutions");
    else puts("No solution");
    return 0;
}

==问题二：if (fabs(a[t][c]) < eps) continue;如何理解。==

假设 c表示列，r表示行，此时我们进行到了 c=2 r=2
1 0 2 3
0 0 3 2
0 0 2 3
你会发现此时r行之下 的c列的绝对值最大值就是0.
说明此时的第c列已经化简好了那么，那么我们就不需要在进行下面的化简操作，
但是此时我们的第r行不用变，此时c加1 那么我们就接着从 第二行 第三列开始找绝对值最大的数。
如果我们的r向后移动了，那么此时我们的第2行是没有化简的，这显然是不对的。
以此为例，r如果向后移动了，此时r=3,c=3 但是此时我们的 第二行 第三个数 是 3 并不是1 这种最简的形态。

==问题三：倒着推解是如何来的==

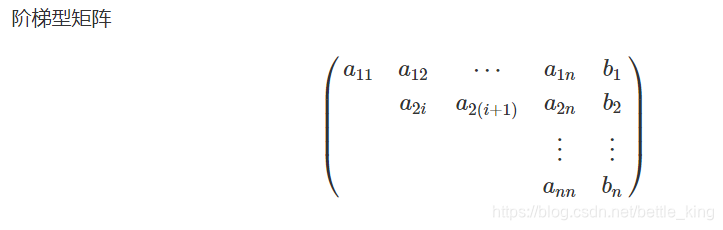
当有唯一解的时候，我们最后的化简一定是这种。
解的最终形式，如下所示:

我们倒着将每一行都简成每一行只有一个1 的形式。 这里模拟一下，代码就懂了。这里不在赘述。

最后，谢谢各位的观看。我们下期再见！！！
CSDN博客: 幽殇默
CSDN博客: 辉小歌
谢谢关注