最近在补全提高课所有题目的题解,宣传一下汇总的地方提高课题解补全计划
题目描述
题目给定一个长度为 n 的一维数组 w[n],表示每个楼房的高度
怪盗基德可以选定任意一个楼房,作为他的起始位置
他可以选择向左或向右出发直到边界,途中不能改变方向
题目要求我们找出一条路径,使得他飞行的路线上,经过的高度递减的楼房子序列长度最大
输出该子序列的长度
题解
这题选比较裸的一道题,我们先来分析一下题目
首先,求一个高度递减的楼房子序列长度最大,其实就是求一个最长下降子序列
然后,这个怪盗基德老哥可以选择任意楼房作为起始位置,接着选择一个方向飞到尽头
于是,我们可以画出如下三种情况:
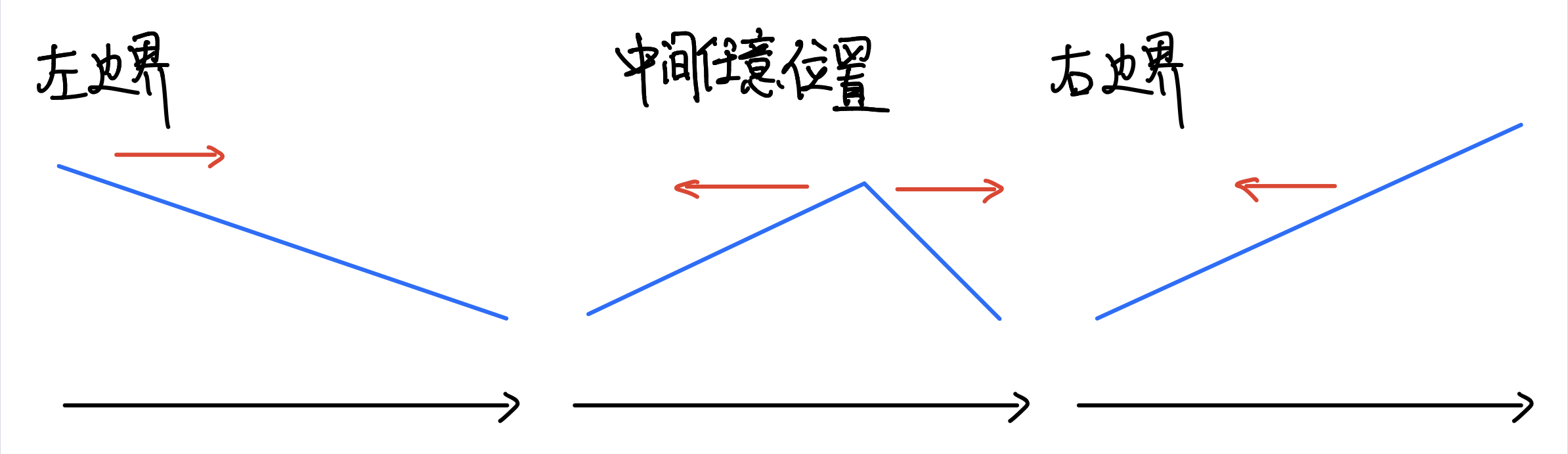
对于左边界情况来说,其实就是中间位置的左侧序列长度为 0 的情况;右边界情况同理
所以,我们只需讨论中间情况即可(两侧边界情况是该情况的子集)
于是,对于任意位置 x,我们分别需要求出以他为右端点的最长上升子序列,以及作为左端点的最长下降子序列
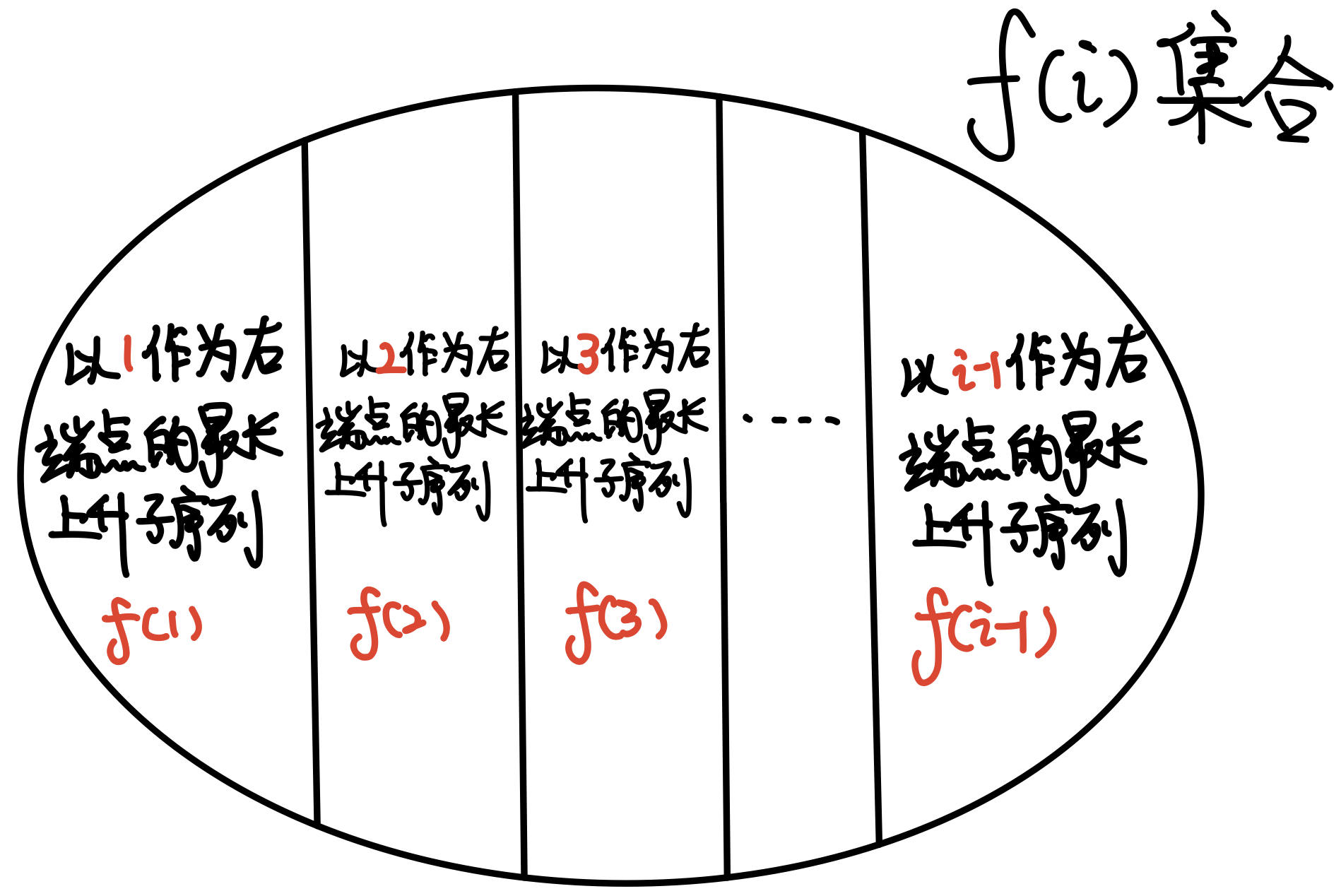
而DP中经典的最长上升子序列模型f[i]的状态表示就是以i为端点的最长上升子序列
由此我们通过线性DP,可以求出任一点的左侧最长上升和右侧最长下降
两者取一个 Max,就是以该点作为起点的最佳飞行方向的最大长度
然后再枚举所有点取一个 Max,就是最佳起点的最大长度,便是本题的答案
这题的DP模型就是经典的最长上升子序列
闫氏DP分析法
{状态表示fi{集合:以第i个位置作为最长上升子序列的右端点的方案 属性:方案的子序列长度最大Max 状态转移fi=max{1,max{∑i−1j=1fj}+1}(ai>aj)
集合划分
Code
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int K, n;
int w[N];
int f_up[N], f_dw[N];
int main()
{
scanf("%d", &K);
while (K -- )
{
memset(f_up, 0, sizeof f_up);
memset(f_dw, 0, sizeof f_dw);
scanf("%d", &n);
for (int i = 1; i <= n; ++ i) scanf("%d", &w[i]);
//最长上升子序列
//哨兵,不设置的话,需要在循环里额外写一条f[i]=1作为初值
w[0] = 0;
for (int i = 1; i <= n; ++ i)
{
for (int j = 0; j < i; ++ j)
{
if (w[i] > w[j]) f_up[i] = max(f_up[i], f_up[j] + 1);
}
}
//反向最长上升
w[n + 1] = 0;
for (int i = n; i; -- i)
{
for (int j = n + 1; j > i; -- j)
{
if (w[i] > w[j]) f_dw[i] = max(f_dw[i], f_dw[j] + 1);
}
}
int res = 0;
for (int i = 1; i <= n; ++ i)
{
res = max(res, f_up[i]);
res = max(res, f_dw[i]);
}
printf("%d\n", res);
}
return 0;
}

#include<iostream> #include<cstring> using namespace std; const int N =110; int w[N],up[N],down[N]; int main() { int t;scanf("%d",&t); while(t--) { memset(up,0,sizeof up); memset(down,0,sizeof down); int res = 0; int n; cin>>n; if(n==1) res =1; for(int i = 0 ;i<n;i++) { scanf("%d",&w[i]); down[i] = 1;up[i] = 1; for(int j=0;j<i;j++) { //up if(w[i]<w[j]) up[i] = max(up[i],up[j]+1); res = max(res ,up[i]); //down if(w[i]>w[j]) down[i] = max(down[i],down[j]+1); res = max(res,down[i]); } } printf("%d\n",res); } }感觉可以更简单一点
同样思路!res初始值可以直接赋1,这样就不用特判n==1的情况了!
为什么在计算上升子序列时,j要从0开始索引而不是1呢
#include[HTML_REMOVED]
#include[HTML_REMOVED]
#include[HTML_REMOVED]
using namespace std;
const int N = 110;
int T,n,a[N],q[N],tt,hh;
int find(int x)
{
int l = hh, r = tt;
while(l < r)
{
int mid = (l +r) /2;
if(q[mid] >= x) r = mid;
else l = mid + 1;
}
return l;
}
int main()
{
ios::sync_with_stdio(false); cin>>T; while(T--) { int res = 0; tt = -1, hh = 0; memset(q,0,sizeof q); cin>>n; for(int i = 1; i <= n; i++) cin>>a[i]; q[++tt] = a[1]; for(int i = 2; i <= n; i++) if(a[i] > q[tt]) q[++tt] = a[i]; else q[find(a[i])] = a[i]; res = tt + 1; tt = -1,hh = 0; q[++tt] = a[n]; for(int i = n-1; i >= 1; i--) if(a[i] > q[tt]) q[++tt] = a[i]; else q[find(a[i])] = a[i]; res = max(res,tt + 1); cout<<res<<endl; } return 0;}
感觉可以优化
f[i] = 1; for (int j = 1; j < i; j++)铅笔把这两行改成了这个,我好菜写了好几道才发现
for (int j = 0; j < i; ++ j)还要加上前面对w的初始化
写的思路好清晰啊
感谢支持 w
求最长下降子序列应该从后往前推吧
对的,是y总数据弱了
这题解挂这误人子弟了5个月,太惭愧了
这题真迷惑。。竟然不会撞楼,可以绕过去。。。我现在才想明白
看到你这句话也才懂hh
我也是hh
hh原来是这样
我刚刚就在想这个问题,我以为是连续的
# 我也是这样,纠结了好久