题目描述

长度偶数序列两两配对(x,y),求使得所有配对差值|x-y|和最小的方案.

ys贪心证明法( =.= )

证明思路

证明
    设贪心解求得差值和为res;最优解值为ans.
    证明目标: res = ans
    证明思路: res >= ans 且 res <= ans
    1.res>=ans
        最优解是所有合法方案的最小值,而贪心解是所有合法方案中的一种,所以res >= ans.
    2.res<=ans
        证明思路:动态调整,每次调整左端贪心解与最优解不同的配对方案,将最优解调整为贪心解,且
    调整过程中数值不增.
        设贪心解与最优解第一个不同配对方案在i处

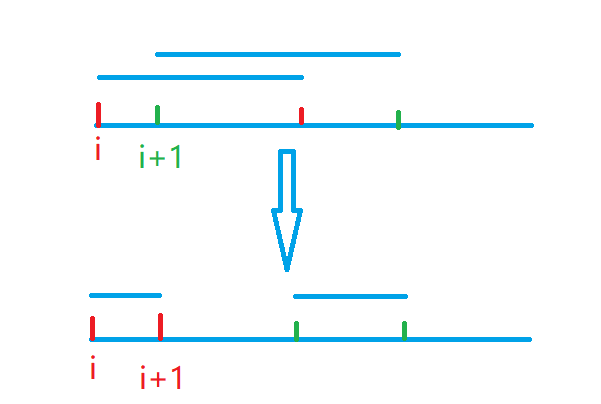
    按贪心方案调整,观察/计算知数值不会增加.
    重复向右端调整下一个不同的配对方案,直到最优方案变成贪心方案,整个过程配对值不会增加,
所以ans>=res
    ==> res = ans

时间复杂度

排序时间0(nlogn)

C++ 代码

#include<cstdio>
#include<algorithm>

using namespace std;

const int N = 1e5 + 10;

int n;
int a[N];

int main()
{
    scanf("%d",&n);
    for( int i = 0; i < n; i++ )    scanf("%d",&a[i]);

    sort(a,a+n);

    long long res = 0;
    for( int i = 0; i<n; i+=2 )
    {
        res += a[i+1] - a[i];
    }
    printf("%lld\n",res);
    return 0;
}