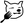首先最小修改成本问题等价于【找到一个最小总和 sum，使得对数为 n / 2】

需要证明如下内容：

1. 修改必然发生在数值不相等的数之间，即原本已经成对的数值不会被修改

   考虑 a1,a2,..ak,an 序列，假设原本的 sum = a1 + a2 + … + an，由于我们只能做加法，因此修改我们必然是让不成对的数 a，靠近另外一个不成对的数 b 。这时候修改已经成对数只会带来无效成本。

2. 现在只要考虑不成对的数字，将不成对的数字进行排序，修改必然发生在前一个数（将其修改成后一个数）

   还是用刚刚的 sum 举例，修改成最靠近一个数，产生的成本最低，每个【新组成的对】的成本均取最低，即可得全局最低

import java.util.*;
class Main {
    public static void main(String[] ar) {
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int[] cnts = new int[10009];
        for (int i = 1; i <= n; i++) {
            cnts[sc.nextInt()]++;
        }
        int ans = 0;
        List<Integer> list = new ArrayList<>();
        for (int i = 1; i < 10009; i++) {
            int t = cnts[i];
            if (cnts[i] % 2 != 0) {
                while (t-- > 0) list.add(i);
            }
        }
        int m = list.size();
        for (int i = 0; i < m; i += 2) {
            int a = list.get(i), b = list.get(i + 1);
            ans += (b - a);
        }
        System.out.println(ans);
    }
}