题目描述

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，”ace”是”abcde”的一个子序列，而”aec”不是）。

进阶：

如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

样例

输入：s = "abc", t = "ahbgdc"
输出：true

输入：s = "axc", t = "ahbgdc"
输出：false

算法1

(双指针解法) $O(n)$

用一个指针来遍历s 字符串,另一个指针用来遍历t 字符串即可

时间复杂度

遍历一遍t 字符串,时间复杂度:O(n)

参考文献

Java 代码

class Solution {
    public boolean isSubsequence(String s, String t) {
    //双指针解法
        int index = 0;//遍历s 的指针

        //遍历t
        for(int i = 0; i < t.length(); i++){
            if(index < s.length()){
                if(t.charAt(i) == s.charAt(index)){
                    index ++;
                }
            }           
        }
        return index == s.length();
    }
}

算法2

(动态规划) $O(n^2)$

这种解法用于:在大量输入s 字符串的情况下,因为每次输入一次s 字符串,都得遍历一次t 字符串,输入次数 x t 字符串长度 = 整体时间复杂度,所以输入的次数越多,时间复杂度越大。那要怎么解决怎么问题呢?
如果我们提前知道了t 字符串各个字符串在字符串中的位置,那每一次寻找的时候就能直接找到这个字符的话,时间复杂度就会很低了。但要注意一个问题: t 在查找的过程中只能从前往后找,比如:s = “abc”, t = “ahbgdc”,当我们从t 字符串中找到了’a’.那么后面的字符串就只能从’a’ 后面的字符串中找了。
所以我们设计的dp 数组中,记录的就是t 字符串中以某一个字符开头,当前字符串以及其后面的字符第一次出现的位置。

对于dp 数组的设计: 一维数组代表t 字符串中每一个字符的索引,二维数组设计成一个26 大小的数组,代表’a’ - ‘z’,记录从t[i] 开始的字符串中,字符’a’ - ‘z’ 第一次出现的位置.

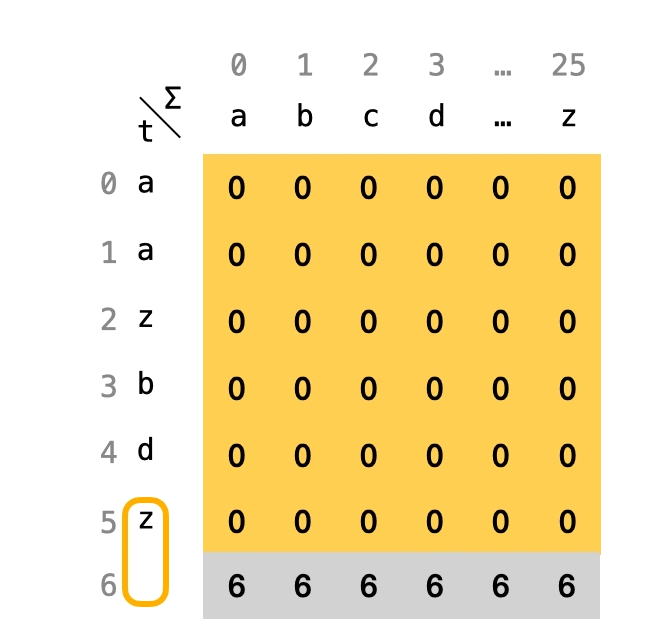
动态规划3 要素:
1.状态定义: dp[i][j] 表示字符串t 从位置i 开始,第j 个字符串开始第一次出现的位置

2.状态转移方程: dp[i][j] = dp[i + 1][j] t[i] != j; dp[i][j] = i,t[i] == j

3.初始条件: dp[nums.length + 1][j] = nums.length + 1;

时间复杂度

O(m×∣Σ∣+n),O中 n为 s 的长度，m 为 t 的长度，Σ 为字符集，在本题中字符串只包含小写字母，∣Σ∣=26。预处理时间复杂度 O(m)，判断子序列时间复杂度 O(n)。
如果是计算 k 个平均长度为 n 的字符串是否为 t 的子序列，则时间复杂度为 O(m ×∣Σ∣+k×n)

参考文献

Java 代码

class Solution {
    public boolean isSubsequence(String s, String t) {

        int[][] dp = new int[t.length() + 1][26];

        //给dp 最后一行的所有列填上: t.length()
        //代表这一行不存在t 字符串的任何字符
        for(int i = 0; i < dp[0].length; i ++){
            dp[t.length()][i] = t.length();
        }

        //从后往前递推dp 数组
        for(int i = t.length()-1; i >= 0; i--){
            for(int j = 0; j < dp[0].length; j++){
                //如果在dp 的当前行(i: 代表t 索引)的列中找到对应的字符(二维数组的索引j + ‘a')
                //那么此时的j 位置对应的值就是i: 代表以i 索引的字符开头的字符串中,i 字符第一次出现的位置
                if(t.charAt(i) == j + 'a'){
                    dp[i][j] = i;
                }else{
                    //如果没有找到当前字符在字符串
                    dp[i][j] = dp[i+1][j];
                }
            }
        }

        //从上面for出来,此时的dp[0] 就记录着: 以字符t[0] 开头的字符串中,后面的字符第一次出现的位置

        int index = 0; //遍历s 的指针

        //遍历dp 数组的一维数组: 对应s 字符串
        for(int i = 0; i < s.length(); i++){
            if(dp[index][s.charAt(i) - 'a'] == t.length()){
                return false; //说明当前以dp[index] 字符开头的字符串中没有当前字符:s.charAt(i) - 'a'
            }else{
                //如果找到了当前s 字符串中的字符,比如dp[0] 中找到了s 字符串的第一个字符,那么要找到s
                //字符串的第二个字符,就得以从dp[0] 中找到的字符中记录的索引的下一位开始寻找,也就是:
                //s = "abc", t = "ahbgdc", s 的'a' 和t 的第一个'a' 配对了,要找到s 的'b' 就得从
                //t 的'h' 开头的字符串开始寻找
                index = dp[index][s.charAt(i) - 'a'] + 1;
            }
        }

        return true;
    }
}