最近在补全提高课所有题目的题解，引荐一下汇总的地方提高课题解汇总

题目描述

题目给定一个 $n \times n$ 的矩阵，矩阵中的每个格子上有一个价值为 $w$ 的物品

给定起点 $(1,1)$，终点 $(n,n)$，每次规定只能向右或向下走

我们可以从起点出发两次，但同一个格子在两次路径中都经过的话，他的物品价值只会被累加 $1$ 次

问两次路线，途径格子的物品的总价值最大是多少

题解

看到题目，就会发现，又是一道数字三角形模型的题目

但不同以往，这次允许我们从起点出发两次，所以需要在原来的基础上做一些变形

关于当前的状态如何表示：

一开始一般会想到用四维数组f[x1][y1][x2][y2]来记录两条路线当前走到位置的坐标

但是题目中有一个限制，那就是对于两次路线都经过的点，其价值只会被累加一次

如果用四个坐标来表示当前的状态，那我们还需要额外开一维来记录当前矩阵中哪些格子被取过数了

即 f[x1][y1][x2][y2][1 << (n * n)]

关于这种状态压缩的做法我就不再展开了，明眼人都看出来，时间复杂度和空间复杂度会爆掉

题目要求我们从起点先后出发两次

但我们可以规定两次是同时出发的，因为这两种方案的所有路线都是一一对应的

为什么这么映射呢？因为这样子做的话，我们可以轻松的处理两次路线走到同一个格子的情况

由此我们就可以把路径长度，作为DP的阶段

每个阶段中，我们同时把两条路径扩展一步，即路径长度加 $1$ ，来进入下一个阶段

而路径长度加$1$后，无非就是向下走一格或是向右走一格，对应横纵坐标的变换

根据$k,x_1,y_1,x_2,y_2$的关系，我们可以获得如下等式

$$ x_1 + y_1 = x_2 + y_2 = k $$

获得上述等式以后，我们就可以通过三个维度来描述状态了，分别是$k, x_1, x_2$

于是，状态的初值为f[2][1][1]，目标状态为f[2 * n][n][n]

则对于如何判断两次路线走进了同一个方格里，可以通过$x_1 = x_2$来判断了

1. 当$x_1 \ne x_2$，当前两条路线走到的格子不是同一个，则$\mathrm{w} = w(x_1,k-x_1) + w(x_2,k-w_2)$
2. 当$x_1=x_2$，当前两条路线走到了同一个格子中，则$\mathrm{w} = w(x_1,k-x_1)$

而状态转移，基本参照数字三角形的模型即可，具体的我贴出闫氏DP分析法思维导图

闫氏DP分析法

$$ \begin{cases} 状态表示f_{k,i,j} \begin{cases} 属性: 路径长度为k,第一条路线到x_1=i,第二条路线到x_2=j的所有方案 \\\ 集合: 方案中的路线经过的所有物品的总价值最大 Max \end{cases} \\\ 状态转移 f_{k,i,j} = max\{f_{k-1,i,j},f_{k-1,i-1,j},f_{k-1,i,j-1},f_{k-1,i-1,j-1}\} + w \end{cases} $$

集合划分

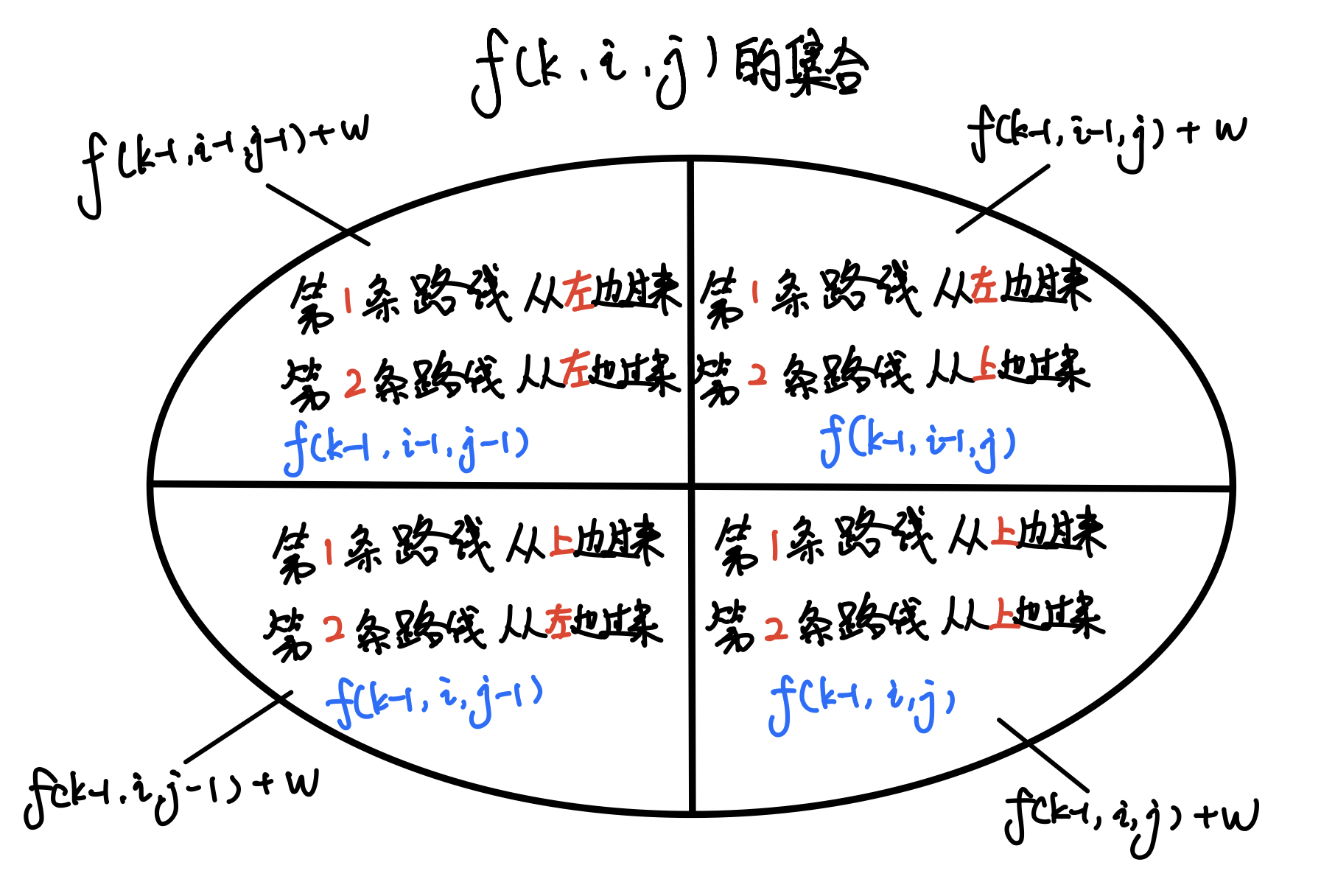
Code(迭代三个状态写法)

#include <iostream>

using namespace std;

const int N = 15, M = 2 * N;

int n;
int a, b, c;
int w[N][N];
int f[M][N][N];

int main()
{
    //input
    cin >> n;
    while (cin >> a >> b >> c, a || b || c) w[a][b] += c;
    //dp
    for (int k = 2; k <= 2 * n; ++ k)
    {
        for (int i = 1; i <= n; ++ i)
        {
            for (int j = 1; j <= n; ++ j)
            {
                int &t = f[k][i][j];
                //越界判断
                if (k - i <= 0 || k - i > n || k - j <= 0 || k - j > n) continue;
                //判断是否两条路线走到了相同的格子
                int v = w[i][k - i];
                if (i != j) v += w[j][k - j];//如果两条路线走到一个格子中，则只累加一次物品的价值
                t = max(t, f[k - 1][i - 1][j - 1]);
                t = max(t, f[k - 1][i][j - 1]);
                t = max(t, f[k - 1][i - 1][j]);
                t = max(t, f[k - 1][i][j]);
                t += v;
            }
        }
    }
    //output
    cout << f[2 * n][n][n] << endl;
    return 0;
}

Code(记忆化搜索写法)

#include <iostream>
#include <cstring>

using namespace std;

const int N = 15, M = 2 * N, INF = 0x3f3f3f3f;

int n;
int a, b, c;
int w[N][N];
int f[M][N][N];

int dp(int k, int i, int j)
{
    if (f[k][i][j] >= 0) return f[k][i][j];
    //起点判断
    if (k == 2 && i == 1 && j == 1) return f[k][i][j] = w[1][1];
    //越界判断
    if (i <= 0 || i >= k || j <= 0 || j >= k) return -INF;

    //重复格子判断
    int v = w[i][k - i];
    if (i != j) v += w[j][k - j];

    //状态转移
    int &t = f[k][i][j];
    t = max(t, dp(k - 1, i, j));
    t = max(t, dp(k - 1, i - 1, j));
    t = max(t, dp(k - 1, i, j - 1));
    t = max(t, dp(k - 1, i - 1, j - 1));

    return f[k][i][j] = t + v;
}
int main()
{
    memset(f, -1, sizeof f);
    cin >> n;
    while (cin >> a >> b >> c, a || b || c) w[a][b] += c;
    cout << dp(2 * n, n, n) << endl;
    return 0;
}