题目描述

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环，边权可能为负数。

求最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

给定一张边带权的无向图 G=(V,E)，其中 V 表示图中点的集合，E 表示图中边的集合，n=|V|，m=|E|。

由 V 中的全部 n 个顶点和 E 中 n−1 条边构成的无向连通子图被称为 G 的一棵生成树，其中边的权值之和最小的生成树被称为无向图 G 的最小生成树。

输入格式
第一行包含两个整数 n 和 m。

接下来 m 行，每行包含三个整数 u,v,w，表示点 u 和点 v 之间存在一条权值为 w 的边。

输出格式
共一行，若存在最小生成树，则输出一个整数，表示最小生成树的树边权重之和，如果最小生成树不存在则输出 impossible。

数据范围
1≤n≤105,
1≤m≤2∗105,
图中涉及边的边权的绝对值均不超过 1000。

样例

输入样例：
4 5
1 2 1
1 3 2
1 4 3
2 3 2
3 4 4
输出样例：
6

Kruskal算法的过程：
Kruskal算法基本思想是把森林合并成一棵树，什么是把森林合并成一棵树呢？就是在初始的状况下，我们认为每一个顶点都是一棵树，然后通过不断地把边收入树中，就把两棵树（两个结点）合并成了一棵树，最后要把所有的结点都并成一棵树。
以边为基础，从边入手，每次找所有未访问过的边中权重最小的边，在下图中，两条边权重为1，直接收入树中。

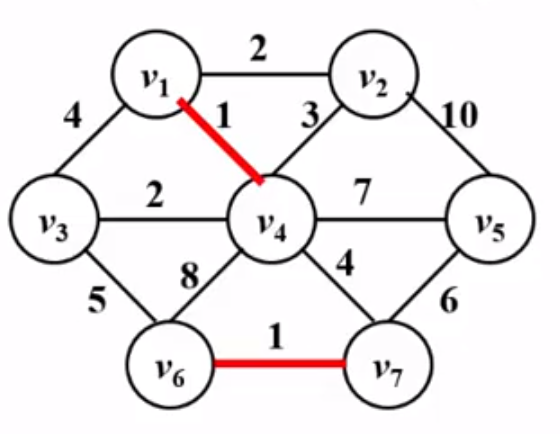
下面继续寻找权重最小的边，发现有两条权重为2的边，也可以收入树中，如下图

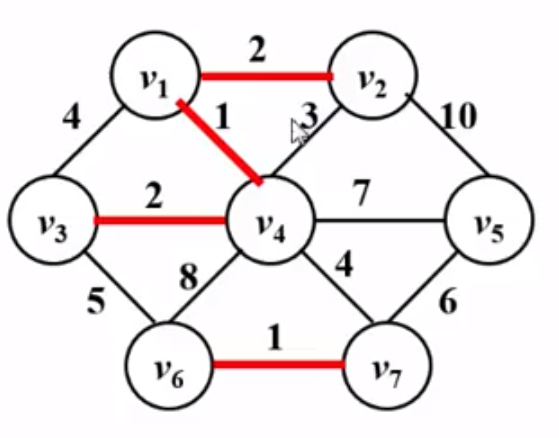
继续找，此时我们发现权重最小的边是3，但是3不能收入树中，因为收入树中后构成了回路（根据树的定义知：树中不允许有回路），同理，v1与v3之间的边也因构成回路而不能收入树中。接下来，我们发现v4到v7权重为4的边权重最小且收入树中后不会构成回路，所以将4收入树中，如下图：

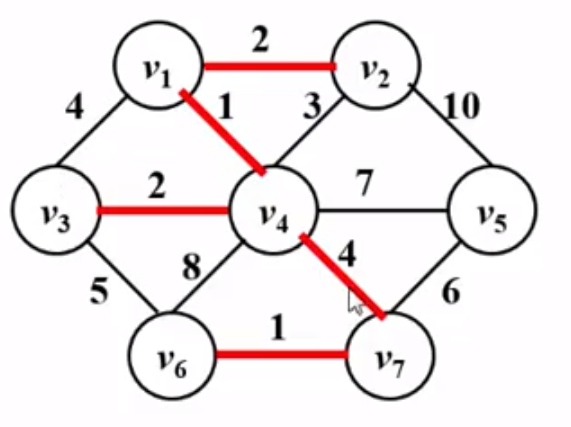
再下来，v3与v5之间权重为5的边权重最小，但是会构成回路，不能收入树中，所以剩下满足条件的就是v5到v7权重为6的边，将其收入树中，如下图：

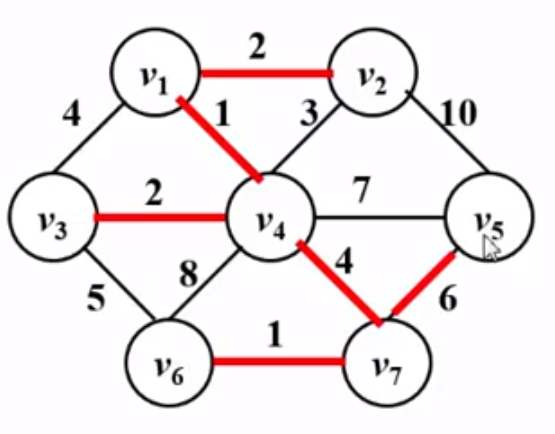
到此为止，树中已经有了6条边，一共7个结点，所以我们已经求出了最小生成树。（n个结点的最小生成树有n-1条边）

步骤：
1.将所有边按权重从小到大排序
2.循环迭代m次，枚举每条边a,b,如果a,b不连通，则将这条边加入集合中（说白了就是在a,b之间加一条边，这里要用到并查集的知识）

Kruskal算法适用于稀疏图
时间复杂度为 $O(mlogm)$ 其中m为边数

C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010, M = N * 2, INF = 0x3f3f3f3f;

int n,m;
int p[N]; //并查集数组

struct Edge
{
    int a,b,w;
    //重载运算符
    bool operator< (const Edge &W)const
    {
        return w < W.w;
    }
}edges[M];

//并查集 + 路径压缩 
int find(int x)
{
    if(x != p[x]) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    //1.将边按权重排序
    sort(edges, edges + m);

    for(int i = 1; i <= n; i ++ ) p[i] = i; //初始化并查集数组

    //2.枚举每条边a->b，如果不连通，则将a将入最小生成树
    int res = 0, cnt = 0;
    for(int i = 0; i < m; i ++ )
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if(a != b) //这一步可以自动滤去回路的情况，因为如果a,b在同一个集合（树）中，就不会再向a,b之间加边了
        {//整个最小生成树一开始只有一个结点，不断往进加边将多个结点合并成树
            p[a] = b;
            res += w;
            cnt ++;
        }
    }
    if(cnt < n - 1) return INF; //如果枚举的边数小于n-1，说明有结点没有被加入，即图不连通，最小生成树不存在
    return res;
}

int main()
{
    scanf("%d%d",&n,&m);

    for(int i = 0; i < m; i ++ )
    {
        int a,b,w;
        scanf("%d%d%d",&a,&b,&w);
        edges[i] = {a,b,w};
    }

    int t = kruskal();
    if(t == INF) puts("impossible");
    else printf("%d\n", t);

    return 0;
}