环形dp的常见做法和区间dp模板题

区间dp模板参考 AcWing 282. 石子合并

环形序列与一般的直线序列有什么不同呢？

不同之处： 环形序列首尾两个端点可以合并。
相同之处：一样是相邻的子区间进行合并

那么如何用区间dp方法解决环形序列的问题呢？

环形序列用n个点合并n - 1次得到的模型是:

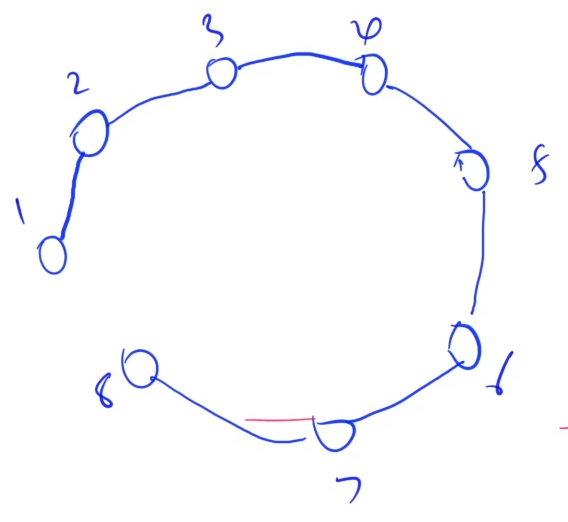
核心思路

合并到最后得到的环形序列就会剩一个缺口，那么对于不同的缺口位置，一共可以组成若干种不同的序列，那么一般用两段重复的直线序列去模拟环形序列:
例如:

缺口在节点1和节点8之间的环形序列，就可以用直线序列的"1 - 8"序列去表示;

缺口在节点 1和节点2 的之间的环形序列，就可以用直线序列的"2 - 1"序列去表示;

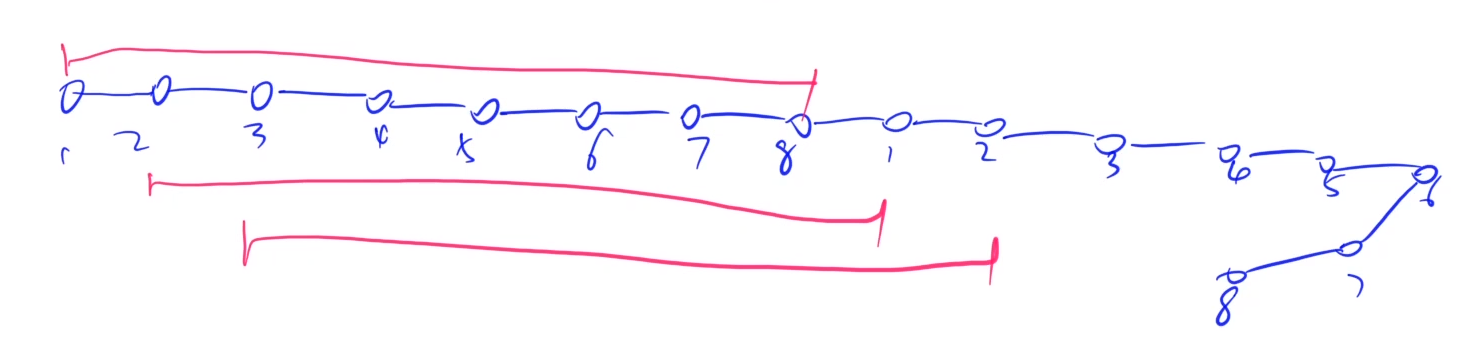
tips: 总结环形问题是否都可以这样解决，处理决定多数环形问题

c++代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 410,INF = 1e8,BNF = -1E8;
int w[N]; //用于保存石头，用两端重复的石头序列去模拟环形的序列
int f[N][N];  //f[i][j]表示所有将i,j合成一堆的所有方案的最小得分
int g[N][N]; //g[i][j]表示所有将i,j合成一堆的所有方案的最大得分
int s[N]; //前缀和数组
int n;
int main(){
    cin >> n;
    for(int i = 1;i <= n;++i){
      cin >> w[i];
      w[i + n] = w[i];
    } 

    for(int i = 1;i <=2 * n;++i){
        s[i] = s[i - 1] + w[i];
    }

    memset(f,0x3f,sizeof f);
    memset(g,-0x3f,sizeof g);

    for(int len = 1;len <= n;++len){
        //枚举长度为len的所有区间的左端点
        for(int l = 1;l + len - 1 <= 2 * n;++l){  //前提是区间的右端点不能越界
            //当前区间的右端点
            int r = l + len - 1;
            //枚举当前区间的分隔点
            if(len == 1) f[l][r] = g[l][r] = 0;
            else{
                for(int k = l;k < r;++k){
                    f[l][r] = min(f[l][r],f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);
                    g[l][r] = max(g[l][r],g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);
                }
            }
        }
    }

    int maxn = -1e8, minn = 1e8; 
    //枚举所有长度为n的区间
    for(int i = 1;i <= n;++i){  //枚举左端点
        maxn = max(maxn,g[i][i + n - 1]);
        minn = min(minn,f[i][i + n - 1]);
    }

    cout << minn << endl << maxn << endl;
    return 0;
}