最近在补全提高课所有题目的题解，引荐一下汇总的地方提高课题解汇总
题目描述
本题大意上给定一个 $n \times n$ 的矩阵，让我们从左上角出发，最终走到右下角
走过的方块数量的不能超过 $2n - 1$ 个
求所有路线中，经过的方块的总价值最少的路线
题解
这题一看很像爆搜啊，但是直接爆搜的时间复杂度是 $2^{10000}$，必然会超时
我们可以细看一下题目，总结一些性质出来
本题的起点是左上角的方块 $(1,1)$，而终点是右下角的方块 $(n,n)$
而每次移动，只能走到四相邻的格子中
四相邻：
我们常在一个矩阵中说四相邻，说的就是以当前格子为中心，上、下、左、右四个方向相邻的格子
也就是对于$(x,y)$来说的$(x-1,y),(x+1,y),(x,y-1),(x,y+1)$的四个格子
因此，我们在矩阵中找任意两个点之间的距离，用到的不是欧式距离，而是曼哈顿距离
欧式距离：
在欧氏空间中，传统意义上的距离，$d_o = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2}$
曼哈顿距离：
两个点在标准坐标系上的绝对轴距总和，$d_m = |x_1-x_2| + |y_1-y_2|$
这题用的就是曼哈顿距离
我们可以模拟一下$(1,1)$到$(2,2)$的曼哈顿距离，答案是$2$
而我们从$(1,1)$出发走到$(2,2)$的最短距离路线分别是
$(1,1)->(1,2)->(2,2)$或者$(1,1)->(2,1)->(2,2)$，路线长度也是$2$
而对于起点的$(1,1)$到终点$(n,n)$，它们之间的曼哈顿距离是$2n - 2$
而本题又要求我们在 $2n - 1$ 的时间内，从起点走到终点
因此，得出结论，我们的走的路线不是完全随机的，而是遵循最短路的原则走的
也就是说，每次移动，至少要使曼哈顿距离缩短 $1$
于是，规定了我们每次在不越过边界的情况下只能向右或向下移动
总结出该条性质以后，本题的模型就可以完全套用AcWing 1015. 摘花生了
如果想要知道这个$\mathrm{dp}$模型的详细推导，可以参考我上面给出的这篇博客
具体的我直接贴出完整闫氏DP分析法思维导图，供大家参考
闫氏DP分析法
$$ \begin{cases} 状态表示\mathrm{f(i,j)} \begin{cases} 属性: 从起点出发，走到第\mathrm{i}行第\mathrm{j}列的所有方案 \\\ 集合: 方案中的路线经过的所有物品的总价值最小 Min \end{cases} \\\ 状态转移 f(i,j) = min\{f(i - 1, j), f(i, j - 1)\} + w(i,j) \end{cases} $$
集合划分
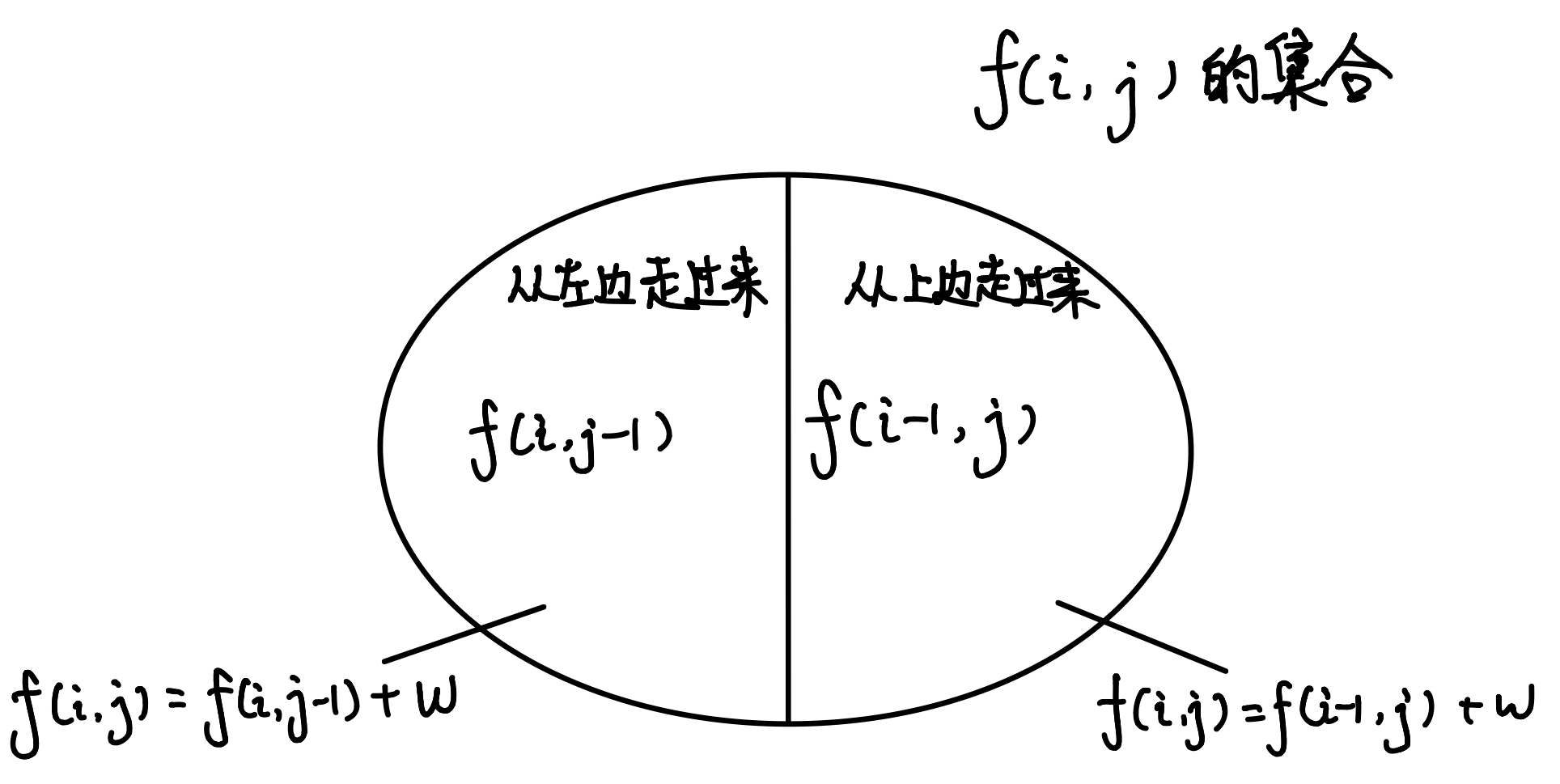
这题不同于摘花生的地方在于，他的属性是最小值，因此需要在代码上作出一点点改变
例如，需要先把所有状态初始化为正无穷，初始化状态的起点（dp求最小值必须要的步骤）
以及，状态转移时的越界判断
Code(循环写法)
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110;
int n;
int w[N][N];
int f[N][N];
int main()
{
//input
cin >> n;
for (int i = 1; i <= n; ++ i)
{
for (int j = 1; j <= n; ++ j)
{
cin >> w[i][j];
}
}
//initialize
memset(f, 0x3f, sizeof f);
f[1][1] = w[1][1];
//dp
for (int i = 1; i <= n; ++ i)
{
for (int j = 1; j <= n; ++ j)
{
f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);
f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]);
}
}
//output
cout << f[n][n] << endl;
return 0;
}
Code(记忆化搜索写法)
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110, INF = 0x3f3f3f3f;
int n;
int w[N][N];
int f[N][N];
int dp(int x, int y)
{
if (f[x][y] >= 0) return f[x][y];
if (x == 1 && y == 1) return w[x][y];
if (x < 1 || y < 1) return INF;
int t = INF;
t = min(t, dp(x - 1, y));
t = min(t, dp(x, y - 1));
return f[x][y] = t + w[x][y];
}
int main()
{
//input
cin >> n;
for (int i = 1; i <= n; ++ i)
{
for (int j = 1; j <= n; ++ j)
{
cin >> w[i][j];
}
}
//dp
memset(f, -1, sizeof f);
cout << dp(n, n) << endl;
return 0;
}
为什么这道题不能用这种状态转移方程 f[i][j] = min(f[i][j - 1], f[i - 1][j]) + w[i][j];
f[i][j] = min(f[i][j], f[i - 1][j] + w[i][j]);
f[i][j] = min(f[i][j], f[i][j - 1] + w[i][j]); 这两种状态转移方程有什么区别吗
我这样写是为了避免特判起点
你的那种写法的话，需要额外特判起点
当然还有一种更简便的写法，用
algorithm库来完成：里面加一个f[i][j] ，就是为了防止边界问题 对吗
是为了不用特判起点，我的代码里把起点的赋值写在外面了hh
懂了 太感谢了hh
为什么这里要考虑边界问题，但摘花生那道题就不需要考虑了？两道题不都是起点终点一样的吗？
因为商人必须在 $2n - 1$个单位时间穿越出去，所以他不能走回头路，只能一直向右走或者向下走，在第一行和第一列格子上，只能是一直向右走或者向下走得到的，摘花生是可以往下走再左右，然后再网上走的，是可以回头的。
这里考虑边界是因为要求的是最小值，那么计算出来的就可能不从左上角出发的值，而是从别的什么位置出发（在图形外面位置进入边界的），摘花生那个要求最大值，从左上角出发一定是最大的值，不可能再从别的什么位置出发了。 （我个人理解）
摘花生不是也不能走回头路嘛，“Hello Kitty只能向东或向南走，不能向西或向北走。”
因为摘花生是最大值，不需要初始化数组，这题是要找min，如果刚开始是0的话直接错了
#include[HTML_REMOVED]
#include[HTML_REMOVED]
using namespace std;
int grid[110][110], f[110];
int main(){
int n;
cin >> n;
memset(f, 0x3f, sizeof f);
for(int i = 1; i <= n; i)
for(int j = 1; j <= n; j)
cin >> grid[i][j];
}
%%% 太感谢了 QAQ
记忆化搜索的memset可以为0吗，然后递归里面if(f[x][y]>0) return f[x][y];
本题费用都是正数，应该可以
大佬我很疑惑为什么从四个方向选最小值也能ac，按理来说只能从当前位置的左边或者上边选才能正确的
这个代码是已经ac了的
我好像明白了。。这是从上到下行遍历，从左到右列遍历，而f[][]的初始值是0x3f，所以该位置的右边和下方位置由于没被重新赋值过，保持为0x3f(这个值使得右下两个方向的值不会被利用)，所以导致看起来是从上下左右四个方向选，实际也是从左上两个方向选。。
和你
i和j的枚举顺序有关，实际上在转移的时候，f[i+1][j]和f[i][j+1]并没有值如果真的要用到这两个去更新，就违背了动态规划的
无后效性，就不能用 DP 来做了懂了懂了
降维写成一维的改怎么办， for(int j=1;j<=n;j++) dp[j]=min(dp[j],dp[j-1])+a[i][j]; 答案总是不对。。。。
像这样？
明白了明白了，我的边界没说明，谢谢啦。
怎么判断初始值
f[1][1]应该设为多少呢，这里f[1][1] = w[1][1]是怎么想到的？f[1][1]是这个动态规划的 初始状态，也就是 起点所以根据状态的定义：
f[1][1] = w[1][1]第一个代码，循环里的两条语句可不可以合并成 f[i][j] = min(f[i-1][j], f[i][j - 1]) + w[i][j];
可以的，我这里这么写是为了不特判状态的初值
f[1][1]因为
f[1][1]不是从f[0][1]或f[1][0]转移过来的合并的话，具体代码要修改成如下形式
明白了！
为啥不是从f01和f10转移过来，而摘花生是从这两个状态过来的，摘花生
这里需要特判（1，1），如果不特判（1，1）分别可以从（1，0）or（0，1）过来，这两点的值为正无穷，且f[i][j]的属性是min，f[1][1]是从这两个无穷大的数更新过来的，摘花生不用特判的原因是求得max，（1，1）无论从（1，0）or（0，1）来都是0，所以不影响结果不需要特判。
##其实这样写就行了