题目描述

算法1

(暴力枚举) $O(nm)$

简单写个题解吧；
矩阵回文大概意思就是其中一个子矩阵的四个顶点值要相同
问题转化为：四个不同的值要转化为同一个值的最小费用为多少
四个值的最小费用比较抽象先看两个值要转化为相同值的最小费用需要多少？

其实只要选取a,b值中的任意一点作为相同值即可得到他们的最小费用（b-a）;
当求三个点的最小费用时，及把相同值c选取为第三个点值即可得到最小费用（b-a）;

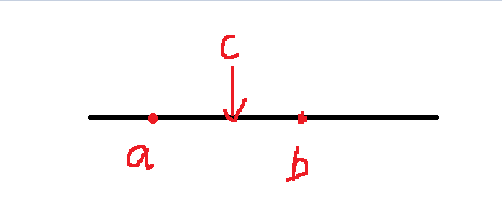
四个值时，选取cd中间值即可得到最小费用；（ab费用最少+cd费用最少）
我们选取第二小的点即可

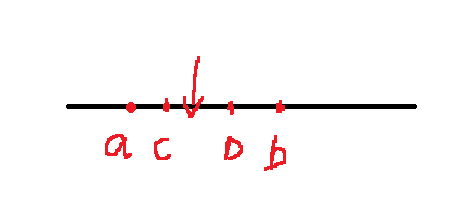
C++ 代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int t;
typedef long long LL;
LL g[N][N];
LL cnt=0;
int main()
{
    cin>>t;
    while(t--){
        cnt=0;
        int n,m;scanf("%d%d",&n,&m);
        for (int i = 1; i <= n; i ++ )for(int j=1;j<=m;j++)scanf("%lld",&g[i][j]);
        for (int i = 1; i <= n; i ++ )for(int j=1;j<=m;j++){
            LL total=max(min(g[i][j],g[i][m-j+1]),min(g[n-i+1][j],g[n-i+1][m-j+1]));
            cnt+=abs(total-g[i][j]);
        }
        cout<<cnt<<endl;
    }
}