非专业排版人士..

解题思路:

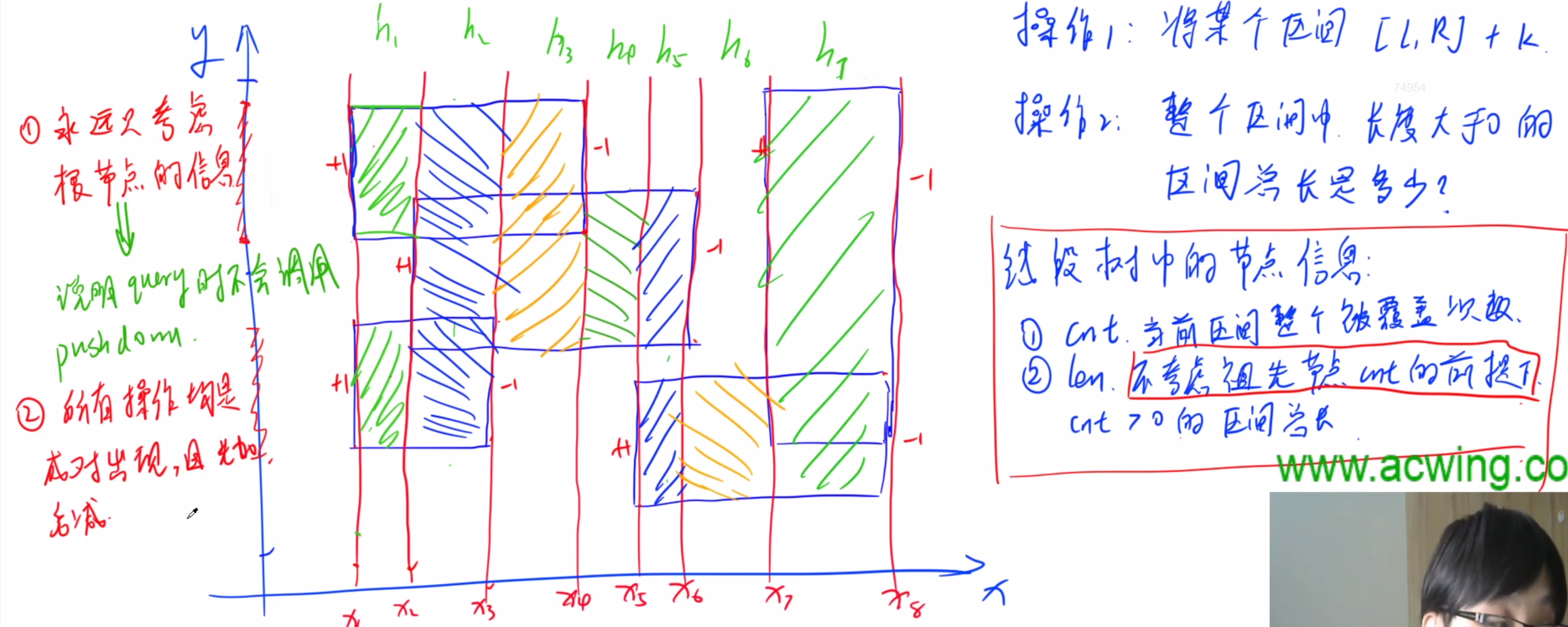
如图, 每遇到矩形的左边, 我们标记这条边的k为+1, 右边则k为-1, 那么, 我们计算有效的线段是 只要那个区间的k>0即可
同时我们的线段树用cnt储存当前段(整段)被覆盖次数, len储存当前段内有效线段总长
然后我们只要用线从左往右扫描, 并记录当前时刻的y方向有效线段长度, 并再每个点乘上x走过的距离得到面积, 加起来就是答案

有了思路, 从main开始看代码注释即可. 至于为什么不需要pushdown(麻烦理解了下面代码再回来看):

分类讨论:

• 对子节点的影响:

  • 当cnt从任意值到非0, 根据modify代码, 我们都会从modify的第一个if进入pushup的第一个if, 然后发现这些情况都只需要算tr[1]的len就够了, 不需要管下面的, 所以不更新不影响结果(因为我们每次计算面积只取tr[1].len)
  • 当cnt从1到0, 那么只需要剔除当前归0的”该一整段”区间对len的影响就行了, 考虑到有可能存在”该一整段”的子区间还在发挥作用(y轴上长度较小且还没到达矩形右边线段的矩形)那这个子区间的len是不需要改变

• 既然不pushdown, 那么会由于不pushdown下去没更新子节点, 导致pushup产生错误吗?
  答: 不会. 分类讨论:

  • 当cnt从任何数到非0数: 根据modify代码, 只有在整段都被覆盖的情况下才会修改当前cnt值, 然后对当前tr[u].cnt=非零值的节点进行pushup, 这样会直接进入pushup的第一个if, 当前u节点的len会被正确地直接计算为整段的长度, 所以哪怕之前的不pushdown下去, 这种情况下的len计算也还是正确的.
  • 当cnt从1到0, 同上根据modify代码, 只有在整段都被覆盖的情况下才会修改当前cnt值, 然后对当前tr[u].cnt=0的节点进行pushup, 把tr[u].len赋值为子节点len的加和或者0(不存在子节点). 我们考虑几何图像, 明显当前情况是出现了矩形右边线段, 所以现在把当前节点整段对len的贡献剔除掉, 所以这样的pushup也是正确的

综上, 我们不需要pushdown也不会影响结果和pushup的正确性

而对于线段树具体如何存储怎么操作:

建立了线段树, 我们再考虑实际线段要怎么存进去, 假设我们存储的是点. 那么当前最小节点是类似[1, 1], [2, 2]这样,
显然他们单独的长度都是0(因为是点)
假设离散化后的ys为 [5.1, 6.2, 8.5, 10.8, …]
考虑线段树内[1, 1], [2, 2]的父节点[1, 2], 我们若需要[1, 2]这个节点的len能够
映射离散化区间里面6.2到8.5的距离的话, 即需要tr[x].r找到8.5, tr[x].l找到6.2 这样看着是可行的
但是这样的话, 当线段树被切分成单位点的时候, 比如若线段树根节点是[0, 2]
要查询[1,2]的长度, 按照线段树国际惯例, 我们下一步会切成[0, 1]和[2, 2], 那么可以发现, 这里我们弄断了两点之间的线段, 且很难继续记录他们之间的关联, 导致难以进行下去

所以, 我们换一种映射方法, 我们考虑令线段树的最小单位是映射相邻两点之间的线段:
同样假设离散化后的ys为 [5.1, 6.2, 8.5, 10.8, …]
考虑线段树区间[0, 0], 我们需要它映射到5.1~6.2这个区间, 同理[1, 1]映射[6.2, 8.5] …
那么, 我们每个线段树最小单位映射的长度, 就应该是ys[tr[t].r + 1] - ys[tr[t].l] 即可
很容易看出, 该做法可以推到更上层的节点也不会出错

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

const int N = 10010;

int n;

// 用于存每一组数据里面的每一条竖线(线段)
struct Segment
{
    double x, y1, y2;
    int k; //标记左右竖线
    bool operator<(const Segment &t)const
    {
        return x < t.x;
    }
}seg[N * 2]; // 每个测试用例包括n组数据(n<=10000), 每组数组是1个矩形, 存2条竖线

struct Node
{
    int l, r; // 左右端点
    int cnt;  // 当前区段(整段)被有效覆盖次数
    double len;  // 当前区间内的有效长度
}tr [N * 8]; // 每个测试用例最多存在, 2n个y坐标再 * 4(线段树)

vector<double> ys;

int find(double y)
{
    return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}

void pushup(int u)
{
    // 如果该"整段"需要算入len
    if (tr[u].cnt) tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];
    // 如果tr[u].cnt等于0其实有两种情况:
    // 1. 完全覆盖. 这种情况由modify的第一个if进入. 
    //    这时下面其实等价于把"由完整的l, r段贡献给len的部分清除掉", 
    //    而留下其他可能存在的子区间段对len的贡献
    // 2. 不完全覆盖, 这种情况由modify的else最后一行进入. 
    //    表示区间并不是完全被覆盖，可能有部分被覆盖,所以要通过儿子的信息来更新
    else if (tr[u].cnt == 0 && tr[u].l != tr[u].r)  //加个==0清晰点
    {
        tr[u].len = tr[u<<1].len + tr[u<<1|1].len;
    }
    else tr[u].len = 0; // 不可再分且cnt等于0, 那就直接安全置0
}

void build(int u, int l, int r)
{
    if (l == r) tr[u] = {l, r, 0, 0};
    if (l != r)
    {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u<<1, l, mid), build(u<<1|1, mid+1, r);
        pushup(u);
    }
}

void modify(int u, int l, int r, int k)
{
    // 线段被包住, 说明整体都是要改的
    if (tr[u].l >= l && tr[u].r <= r)
    {
        tr[u].cnt += k;  // cnt是当前还在计算面积的矩形个数
        pushup(u);
    }
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u<<1, l, r, k);
        if (r > mid) modify(u<<1|1, l, r, k);
        pushup(u);
    }
}

// debug用
void print_tree()
{
    puts("tree:");
    for (int i = 0; i <= ys.size()-2; i++)
    {
        printf("i: %d,  l: %d  r:  %d  cnt:  %d,  len:  %lf\n",
                i, tr[i].l, tr[i].r, tr[i].cnt, tr[i].len);
    }
}

int main()
{
    int T = 1;
    // 测试用例组数不定, 直到n为0才停止
    while (scanf("%d", &n), n)
    {
        ys.clear();
        // 每组测试用例有n个矩形输入
        for (int i = 0, j = 0; i < n; i++)
        {
            double x1, y1, x2, y2;
            scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
            seg[j++] = {x1, y1, y2, 1}; //左竖线
            seg[j++] = {x2, y1, y2, -1}; //右竖线
            ys.push_back(y1), ys.push_back(y2); // 离散化压缩空间
        }

        // 离散化
        sort(ys.begin(), ys.end());
        ys.erase(unique(ys.begin(), ys.end()), ys.end());

        // 对该组所有测试用例的y坐标离散后所在区间构造线段树
        // y轴有ys.size()个点, 而我们线段树需要存线段, 这里一共有ys.size()-1个线段
        // 而线段树build是每个单位点为最小单位, 所以最少得build ys.size()-1个点
        // 所以r最小是build(1, 0, ys.size()-2) 实际上r只需要不比这个ys.size()-2小就行
        build(1, 0, ys.size() - 2);
        // 建立了线段树, 我们再考虑实际线段要怎么存进去, 当前最小节点是类似[1, 1], [2, 2]这样,
        // 显然他们单独的长度都是0(因为是点)
        // 假设离散化后的ys为 [5.1, 6.2, 8.5, 10.8, ...] 
        // 考虑线段树内[1, 1], [2, 2]的父节点[1, 2], 我们若需要[1, 2]这个节点的len能够
        // 映射离散化区间里面6.2到8.5的距离的话, 即需要tr[x].r找到8.5, tr[x].l找到6.2 
        // 这样看着是可行的
        // 但是这样的话, 当线段树被切分成单位点的时候, 比如若线段树根节点是[0, 2]
        // 要查询[1,2]的长度, 按照线段树国际惯例, 我们下一步会切成[0, 1]和[2, 2], 那么可以发现, 
        // 这里我们弄断了两点之间的线段, 且很难继续记录他们之间的关联, 导致难以进行下去

        // 所以, 我们换一种映射方法, 我们考虑令线段树的最小单位是映射相邻两点之间的线段:
        // 同样假设离散化后的ys为 [5.1, 6.2, 8.5, 10.8, ...]
        // 考虑线段树区间[0, 0], 我们需要它映射到5.1~6.2这个区间, 同理[1, 1]映射[6.2, 8.5] ...
        // 那么, 我们每个线段树最小单位映射的长度, 就应该是ys[tr[t].r + 1] - ys[tr[t].l] 即可
        // 很容易看出, 该做法可以推到更上层的节点也不会出错


        // 根据x的大小排序, 确定后面遍历是正确的从左到右
        sort(seg, seg + n * 2);

        double res = 0;
        for (int i = 0; i < n * 2; i++)
        {
            // tr[1].len是当前y轴实际使用长度, 乘上x就是面积
            if (i > 0)res += tr[1].len * (seg[i].x - seg[i-1].x);
            // 线段树插入当前y轴上的用到的线段, .k是标记左右竖线
            // 参考上面调用build之前的注释, 从tr去取出真实ys坐标(y轴离散化后)要+1
            // 那么从真实ys坐标找回对应tr内的右点就减回去1
            modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].k);

        }


        printf("Test case #%d\n", T++);
        printf("Total explored area: %.2lf\n\n", res);
    }
    return 0;
}