AcWing 1027.方格取数
设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：
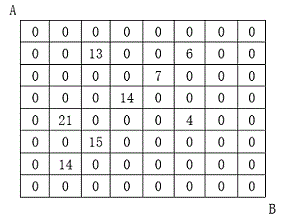
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。
在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。
此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。
输入格式
第一行为一个整数N，表示 N×N 的方格图。
接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。
一行“0 0 0”表示结束。
输出格式
输出一个整数，表示两条路径上取得的最大的和。
数据范围
$N≤10$
输入样例：
8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0
输出样例：
67
题目分析
前置题目及定义
- $k = i_1 + j_1=i_2+j_2$: 两个小朋友同时走, 每个人走的步数和是一样的.
- $f[i_1,j_1,i_2,j_2]$: 由摘花生问题可以推广出从$(1,1),(1,1)$走到$(i_1,j_1),(i_2,j_2)$能获得的最大花生数目.
- 由上面的两条性质可以推出三维的状态转移方程$f[i_1,k-i_1,i_2,k-i_2] \rightarrow f[k,i_1,i_2]$:两个小朋友同时走$k$步,从$(1,1),(1,1)$走到$(i_1,j_1),(i_2,j_2)$能获得的最大花生数目.
- 0:代表小朋友要到下边一个格子
- 1:代表小朋友要到右边一个格子
- 难点:$\forall$格子仅能取一次. 两个小朋友在同一个格子$\rightarrow$必有$i_1==i_2, j_1 == j_2$,而后边状态限制同时走,所以当$i_1==i_2$时便走到同一格.
至此解决状态表示问题, 下面考虑集合划分
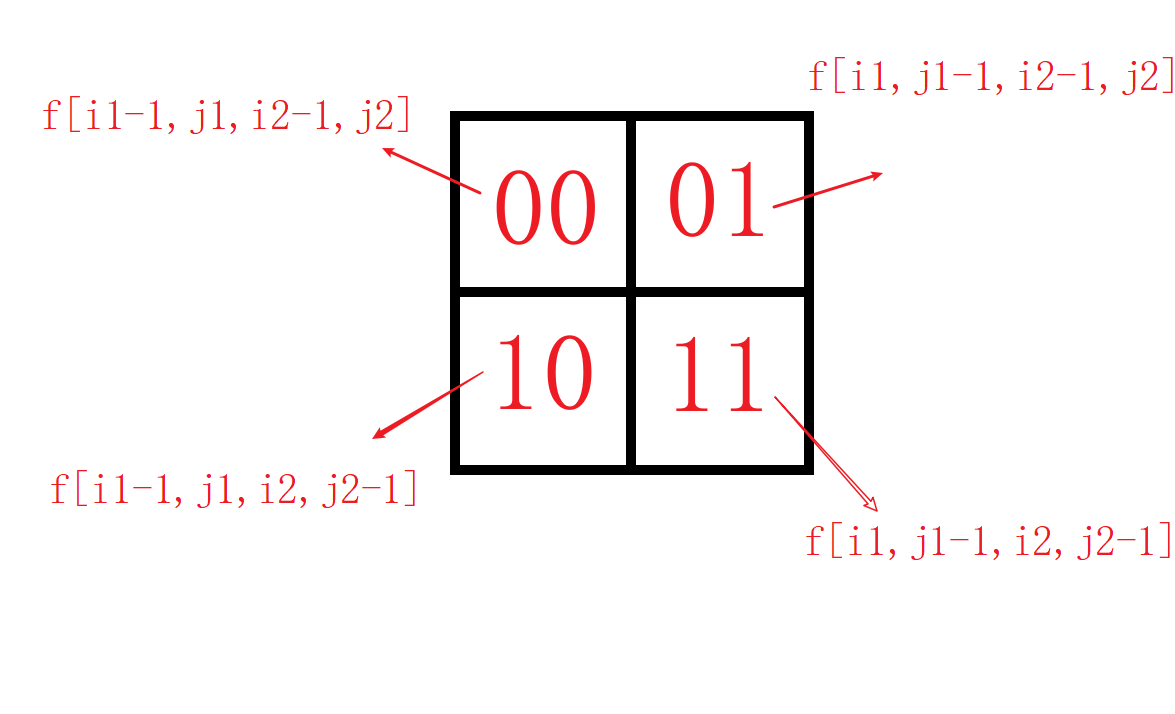
由于上面四种状态类似仅解释一个
$f[i_1-1,j_1,i_2-1,j_2]\rightarrow f[k-1,i_1-1,i_2-1]$:代表两个小朋友都走了$k-1$步,小朋友1要从$(i_1-1,j_1) $到$(i_1,j_1)$,小朋友2要从$(i_2-1,j_2)$到$(i2,j2).$
所以需要判断$(i_1,j_1),(i_2,j_2)$是否是同一个格子,若是则仅需要加上一个权重,反之两个都需要
解决代码思路问题,下面开始解决实现
C++代码
#include <iostream>
using namespace std;
const int N = 15;
int n;
int w[N][N], f[N*2][N][N];
int main() {
cin >> n;
int a,b,c;
while(cin >> a >> b >> c, a || b || c) w[a][b] = c;
for(int k = 2; k <= 2*n; k++) {
for(int i1 = 1; i1 <= n; i1++) {
for(int i2 = 1; i2 <= n; i2++) {
int j1 = k-i1, j2 = k-i2;
if(j1>=1&&j1<=n&&j2>=1&&j2<=n) {
// 不能越界
int &x = f[k][i1][i2];
int t = w[i1][j1];
if(i1!=i2) t += w[i2][j2];
//不重合则需要加两个权重.
x = max(x, f[k-1][i1-1][i2-1]+t);
x = max(x, f[k-1][i1-1][i2]+t);
x = max(x, f[k-1][i1][i2-1]+t);
x = max(x, f[k-1][i1][i2]+t);
//保留最大属性
}
}
}
}
cout << f[n*2][n][n] << endl;
return 0;
}
这里k应该不是走过的步数,走过的步数应该还要减一,所以这里k应该是偏移量之和,这样理解可能会更好一点
俺也觉着应该不是走过的步数之和😮
这个题题意让人看不懂
对的，反正懂意思就行hhh
k是横纵坐标之和
(1, 1) 是k = 2，(n, n) 是k = n + n，这个偏移量概括的很好，一下就想明白了，一圈一圈的往外扩张，最后的答案就是f[n + n][n][n]
请问为什么讲解都说一个点不能重复取，这个题只是说第一次会变成0，没说绝对的不允许重复取吧
当i1 == i2时，限制只让一个人走，不等时两个人同时走。
在提高课的线性DP那有一点问题，摘花生那道题状态转移方程为f[i][j]=max(f[i-1][j]+w[i][j],f[i][j-1]+w[i][j]); 是求最大值的，但是我改写成f[i][j]=max(f[i][j],f[i][j-1]+w[i][j]);
f[i][j]=max(f[i][j],f[i-1][j]+w[i][j]);
就过不了，不知道为什么，因为我看方格取数那块的转移方程就是 x=max(x,f[k-1][i1-1][i2-1]+t);
x=max(x,f[k-1][i1-1][i2]+t);
x=max(x,f[k-1][i1][i2-1]+t);
x=max(x,f[k-1][i1][i2]+t);
这里面就是自己和自己比最大值，求大佬解惑~
怎么过不了我试了一下可以啊
你没有初始化。
f[i][j]=max(f[i][j],f[i][j-1]+w[i][j]);
f[i][j]=max(f[i][j],f[i-1][j]+w[i][j]);
本来就是用来跳过边界的，但你需要手动补上边界，也就是用memset初始化边界。
以及对左上角f[1][1]=w[1][1]的初始化。
01和10的情况是不是写反了…
请问为什么要加&呜呜？我不懂
c++中的引用，相当于起别名，节省代码量的
int &x = f[k][i1][i2] 表示 : 下面所有写
x的部分，可以换成f[k][i1][i2]即
x= max(x, f[k-1][i1-1][i2-1]+t); 等价于f[k][i1][i2]= max(f[k][i1][i2], f[k-1][i1-1][i2-1]+t);这样做单纯是为了写着方便，少打相同的字。
这里的
int &x = f[k][i1][i2]可以换成int x = f[k][i1][i2]吗 加和不加有什么区别&表示引用，不加&就是独立的一个变量x，加了引用
x才能按上述视作等价替换为f[k][i1][i2]是不是这个意思,后面的
x = max(x, f[k-1][i1-1][i2-1]+t);x = max(x, f[k-1][i1-1][i2]+t);里面，如果加了&那么第一个x和第二个x都只是f[k][i1][i2]的意思,如果不加，那么上面的第二个式子里面的x是不是已经被替换为第一个式子里面的最大值了，是不是加了&这个x的值就不会改变，还是说什么意思呀呜呜这样解释吧，加了引用，修改
x的值的同时会修改f[k][i1][i2]，不加引用，只会修改x的值，不会修改f[k][i1][i2]的值;实际上，加了引用后，x指向的就是y的地址，因此修改x的值的同时会修改f[k][i1][i2]。举个例子：
1. 加引用的情况
最后，这样做单纯是为了写着方便，少打相同的字，不用打那么多次f[k][i1][i2]。
感谢你感谢你啦！！我懂了哦嘿嘿
本题不能换
相当于起一个别名
k为什么从2开始
i和j都是从1开始的，而k==i+j，所以k从二开始
为什么要判断越界呢，界限之外的数字不是都没有数据吗
为什么x=max(x,f[k-1][i-1][ii-1])+t;不对x=max(x,f[k-1][i-1][ii-1]+t);对呢？有什么区别吗？
前者是对x 和f[k - 1][i1 - 1][i2 - 1] 取最大值然后加上t，后者是对x 和 f[k - 1][i1 - 1][i2 - 1] + t 取最大值，两者含义不一样
为啥要两个小朋友同时走k步？
当
i1==i2的时候两条路线不是重合了嘛？这时候不符合条件吧？是
1.这样限制才能压缩掉一维嘛？（不理解）
2.因为
(i1,j1)(i2,j2)表示的是终点，终点可以重合我的理解大概是：k应该是同步走，可以想象两个人同时出发，速度相同，也就是走的步数始终一样，但是路径不同
路线可以重合啊，只是重合的话只计算一次
状态表示那里，比如01，这个是代表i1小朋友向右走，i2小朋友向下走的意思对吧
感觉k-1设置的很巧妙
一语双关？？
原本是i1,j1,i2,j2,加入k就算降维了把
为什么每个点只能走一次呢,题目也没规定啊
走过就没有数了啊
为什么int &x=f[k][i1][i2]?
这个操作表示x是f[k][i1][i2]的地址，可以理解为把f[k][i1][i2]换成x
这道题把i2的for条件改成i2<=i1也能过
老哥，通透！
感谢
为什么阶段是k，而不是i1或i2
这个讲清楚了！！！感谢
这个是讲的最清楚的题解了，拜一下！！
有帮助就好
这个引用的作用到底是什么呢
？你的问题描述的不是很清晰，我没有理解想要问问题是什么wuwuwu
哦哦，就是int &x = f[k][i1][i2];那一行， 不过现在理解了，主要是为了让f随之改变
enen
同时也为了省代码量