AC自动机求文章中一共有多少种模板串的模板题
本质上是trie树 + KMP
trie字典树的模板参考: AcWing 835. Trie字符串统计
常见用法就是:
一个常见的例子就是给出n个单词,再给出一段包含m个字符的文章,让你找出有多少个单词在文章里出现过。
简述AC自动机
要搞懂AC自动机,先要有字典树Trie和KMP模式匹配算法的基础知识。
其中,KMP是用于一对一的字符串匹配,而trie虽然能用于多模式匹配,但是每次匹配失败都需要进行回溯,如果模式串很长的话会很浪费时间,
所以AC自动机应运而生,如同Manacher一样,AC自动机利用某些操作阻止了模式串匹配阶段的回溯,将时间复杂度优化到了O ( n ) - n 为文本长度。
AC自动机算法流程
-
1.构造一棵
Trie,作为AC自动机的搜索数据结构。 -
2.构造
fail指针,使当前字符失配时跳转到具有最长公共前后缀的字符继续匹配。如同 KMP算法一样, AC自动机在匹配时如果当前字符匹配失败,那么利用fail指针进行跳转。由此可知如果跳转,跳转后的串的前缀,必为跳转前的模式串的后缀并且跳转的新位置的深度(匹配字符个数)一定小于跳之前的节点。所以我们可以利用 bfs在 Trie上面进行每一层节点fail指针的求解。 -
3.扫描主串进行匹配。
fail数组的定义是:
从a串跳到b串,b串一定是a的字串,那么那么b串一定也是a串某个前缀的后缀,
AC自动机详细图解
1.首先给定模式串 “ash”,“shex”,“bcd”,“sha”,然后我们根据模式串建立如下Trie树:
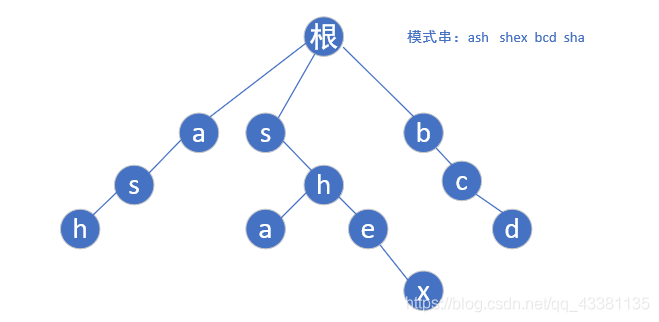
2.然后我们再了解下一步:,
AC自动机就是在Trie树的基础上,增加一个失配时候用的fail指针,如果当前点匹配失败,则将指针转移到fail指针指向的地方,这样就不用回溯,而可以继续匹配下去了.。一般,fail 指针的构建都是用 bfs 实现的。
核心: 当前模式串后缀和fail指针指向的模式串部分前缀相同
例如:题目中给出的总串:yasherhs,模式串为:“shel”和“her”,当比较其中的“her“时,用模式串“hel”进行比较,当我们找到“e”并发现下一个要找的不是“l”,因为模式串“shel”遍历到字母“e”的时候的后缀是"he"可以与另外一个模式串“her”的部分前缀“he”匹配,所以可以跳到”her“的”e“处,接着再进行匹配,发现模式串her就能与主串的”her“匹配上,所以保证当前模式串后缀和fail指针指向的模式串部分前缀相同,就能省去很多比较步骤)
(1)先每个模式串的首字母肯定是指向根节点的:
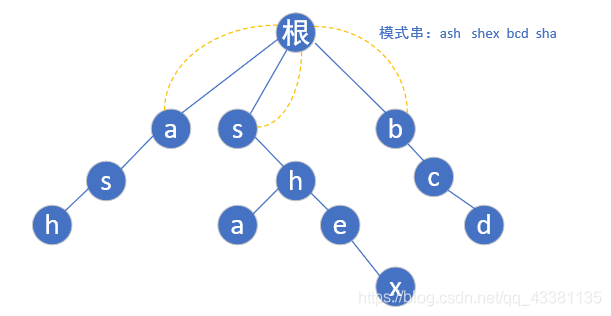
(2)现在第一层 bfs 遍历完了,开始第二层(根节点为第0层)第二层节点 s 是第一层节点 a 的子节点,但是我们还是要从 a - z 遍历,
如果不存在这个子节点,他的树节点值也等于父节点的fail指向的节点中具有相同字母的子节点(如下图中的红色 a ):
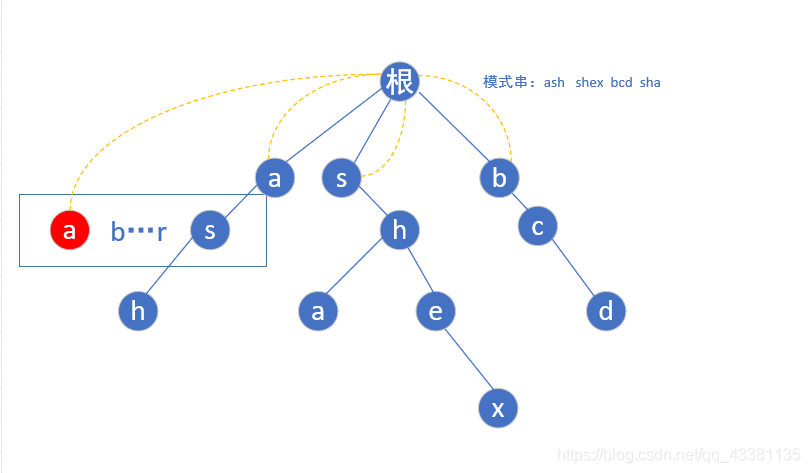
重点:
(3)当我们遍历到 s 的时候,由于存在 s 这个节点,我们就让它的fail指针指向他父亲节点 a 的 fail 指针指向的那个节点(根)的具有相同字母的子节点(第一层的 s),也就是这样:
`如果不存在这个子节点,他的树节点值也等于父节点的fail指向的节点中具有相同字母的子节点(如下图中的红色 a ):
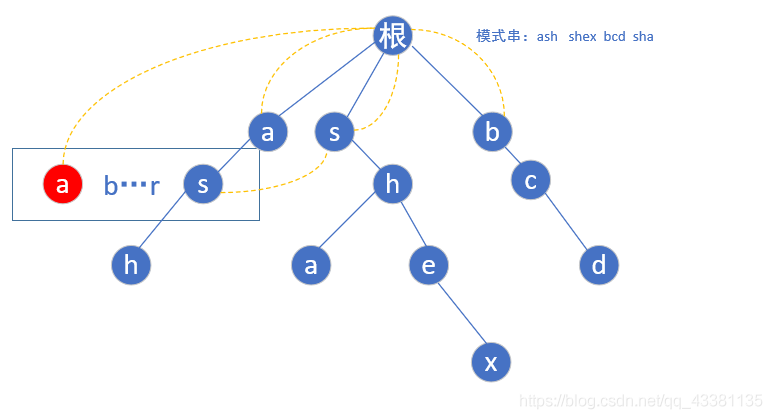
/** 构造fail适配数组 : **/
void build(){ //构造fail数组,bfs
int hh = 0,tt = -1; //队头和队尾指针
//根节点是第0层
for(int i = 0;i < 26;++i){ //第一层的元素全部入队
if(trie[0][i]) que[++tt] = trie[0][i];
}
while(hh <= tt){
int ans = que[hh++];
//枚举当前队头的26个分支
for(int i = 0;i < 26;++i){
if(trie[ans][i]){ //如果存在我们就让它的fail指针指向他父亲节点 a 的 fail 指针指向的那个节点(根)的具有相同字母的子节点
fail[trie[ans][i]] = trie[fail[ans]][i];
que[++tt] = trie[ans][i]; //当前节点入队
}else{ //就算不存在,不跳,他的树节点值也等于父节点的fail指向的节点中具有相同字母的子节点
trie[ans][i] = trie[fail[ans]][i];
}
}
}
}
(4) 按照相同规律构建第二层后,到了第三层的 h 点,还是按照上面的规则,我们找到 h 的父亲节点 s 的 fail 指针指向的那个位置(第一层的 s),然后指向它所指向的相同字母 根 -> s -> h 的这个链的 h 节点,如下图:
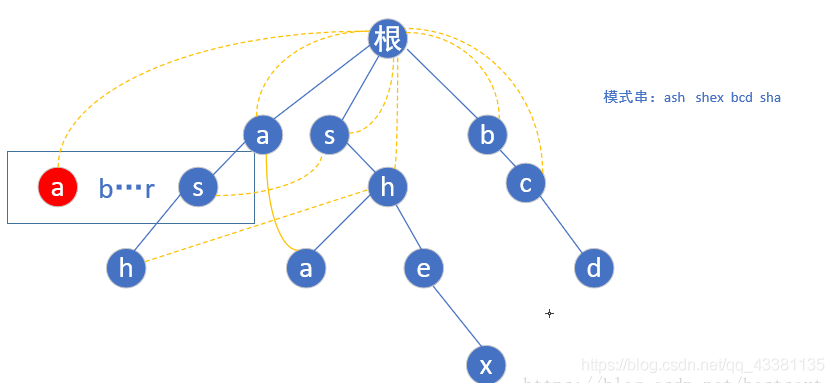
(5)按照如上的规律,完全构造好后的树如下所示:
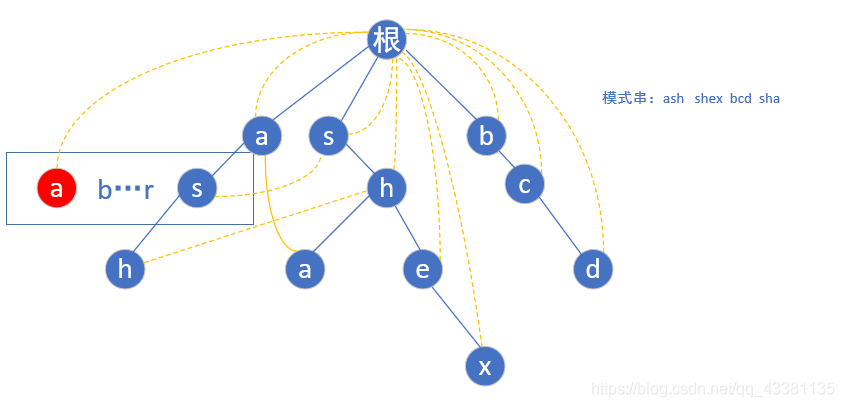
匹配过程:
然后匹配就很简单了,这里以 "ashw" 为例:
我们先用 "ash" 匹配,到 "h" 了发现,"ash" 是一个完整的模式串,则ans++,然后找下一个 "w",可是 "ash" 后面没字母了呀,我们就跳到 "h" 的 fail 指针指向的那个 "h" 继续找,还是没有 ? 再跳,结果当前的 "h" 指向的是根节点,又从根节点找,然而还是没有找到 "w",匹配结束(假设如果有"w"的话,那么模式串"shw"就可以匹配上"ashw")。流程图如下:
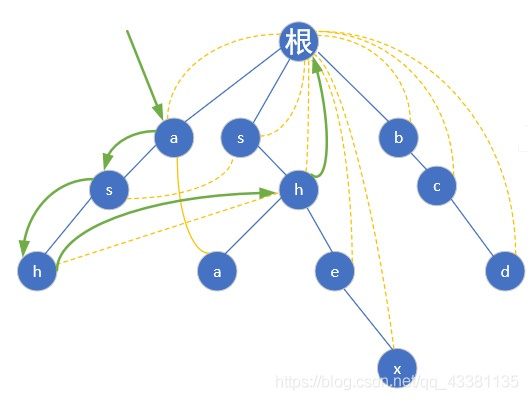
/** 匹配过程:**/
int res = 0;
//j记录当前树节点的指针,初始是根节点
for(int i = 0,j = 0;str[i];++i){ //枚举总串str的每一个字母
int u = str[i] - 'a';
j = trie[j][u]; //跳到下一个树节点
int p = j; //每次从当前树节点开始
//fail[p]所指向的树节点如果有结尾标记可以直接算上,因为当前模式串后缀和fail指针指向的模式串部分前缀相同,所以是包含在里面的
while(p){ //假如模式串"she"可以匹配上,那么匹配到"e"的时候,用fail指针跳到模式串"he"的"e",那么也一定能够匹配"he"
res += cnt[p];
cnt[p] = 0; //去除标记
p = fail[p];
}
}
c++代码
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 10010, S = 55, M = 1000010;
int trie[N * S][26], cnt[N * S], idx; //cnt[i]表示以i + 'a'为结尾的个数 idx为当前树节点的指针
char str[M]; //以"/0"为结尾,所以不用每次都更新
int que[N * S], fail[N * S]; //que[]表示队列 , fail[]为失配指针(下标表示树节点的指针)
int n;
void insert(){
int p = 0;
for(int i = 0;str[i];++i){
int u = str[i] - 'a';
if(!trie[p][u]) trie[p][u] = ++idx;
p = trie[p][u];
}
cnt[p]++;
}
void build(){ //构造fail数组,bfs
int hh = 0,tt = -1; //队头和队尾指针
//根节点是第0层
for(int i = 0;i < 26;++i){ //第一层的元素全部入队
if(trie[0][i]) que[++tt] = trie[0][i];
}
while(hh <= tt){
int ans = que[hh++];
//枚举当前队头的26个分支
for(int i = 0;i < 26;++i){
if(trie[ans][i]){ //如果存在我们就让它的fail指针指向他父亲节点 a 的 fail 指针指向的那个节点(根)的具有相同字母的子节点
fail[trie[ans][i]] = trie[fail[ans]][i];
que[++tt] = trie[ans][i]; //当前节点入队
}else{ //就算不存在,不跳,他的值等于父节点的fail只想的具有相同字母的子节点
trie[ans][i] = trie[fail[ans]][i];
}
}
}
}
int main(){
int t;
cin >> t;
while(t--){
memset(cnt,0,sizeof cnt);
memset(trie,0,sizeof trie);
memset(fail,0,sizeof fail);
idx = 0;
cin >> n;
for(int i = 0;i < n;++i){
scanf("%s",str);
insert();
}
build();
scanf("%s",str);
int res = 0;
//j记录当前树节点的指针,初始是根节点
for(int i = 0,j = 0;str[i];++i){ //枚举总串str的每一个字母
int u = str[i] - 'a';
j = trie[j][u]; //跳到下一个树节点
int p = j; //每次从当前树节点开始
//fail[p]所指向的树节点如果有结尾标记可以直接算上,因为当前模式串后缀和fail指针指向的模式串部分前缀相同,所以是包含在里面的
while(p){ //假如模式串"she"可以匹配上,那么匹配到"e"的时候,用fail指针跳到模式串"he"的"e",那么也一定能够匹配"he"
res += cnt[p];
cnt[p] = 0; //去除标记
p = fail[p];
}
}
cout << res << endl;
}
return 0;
}


tql 清晰明了
核心哪里说的有点乱啊,有点乱跳了
nb,我个菜鸟看懂了qwq
图挺好 一下看懂了
如果不存在这个子节点,他的树节点值也等于父节点的fail指向的节点中具有相同字母的子节点(如下图中的红色 a ): 这句话怎么理解,就是对于不存在的子节点为什么还要赋值
同问
因为万一我需要匹配的串中在这一层需要这个字母,那就无需再回到根节点来重新匹配,直接跳到离他最近的那个相同字母处便可
贼不跑空原则,整一回就别白整,如果后面还有人要问这个问题,就没必要还是递归向上,找 了也白找,不如直接记录下来,再有人问路时就直接告诉它。
答主能请问一下,这是用什么软件做出这种类型的图?
我这个图是之前知乎上介绍ac自动机的帖子上扒下来的。。。
写的真好