算法
(贪心,DP,序列型DP,前缀和) $O(n^2)$
对单调上升和单调下降分别求一遍，取最小值即可。
下面只讨论对单调上升的求法。
引理：
一定存在一组最优解，使得每个 $B_i$ 都是原序列中的某个值。
证明：
假设某个最优解如下图所示，其中 $\{A_i\}$ 是原序列，$\{A’_i\}$ 是将原序列排序后的序列，图中红色圆圈表示每个 $B_i$。
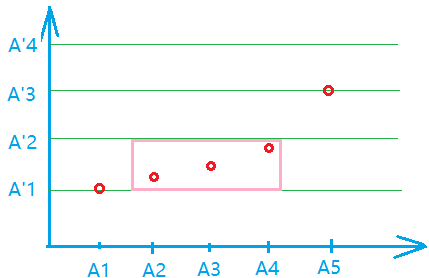
考虑每个位于 $A’_i, A’_{i+1}$之间的一段 $B_i$，比如上图中粉色框中的部分。
则我们在 $\{A_i\}$ 中粉色框对应的这段里统计出大于等于 $A’_{i+1}$ 的数的个数 $x$，小于等于 $A’_i$ 的数的个数 $y$，那么：
- 如果 $x > y$，将粉色框中的 $B_i$ 整体上移，使最高的一个圆圈达到上边界，结果会变好；
- 如果 $x < y$，将粉色框中的 $B_i$ 整体下移，使最低的一个圆圈达到下边界，结果会变好；
- 如果 $x = y$，则上面两种方式均可，结果不会变差；
综上所述，只要存在某个 $B_i$ 的值不在原序列中，我们一定可以将它调整成原序列中的值，且结果不会变差。
证毕。
剩下的问题就比较简单了。用闫氏DP分析法即可。
状态表示：
f[i][j]代表所有给A[1] ~ A[i]分配好了值且最后一个B[i] = A'[j]的方案的集合；f[i][j]的值是集合中所有方案的最小值；
状态计算：
依据倒数第二个数分配的是哪个A'[i]将f[i][j]所代表的集合划分成j个不重不漏的子集：
- 倒数第二个数选取的是
A'[1]的所有方案的结合，最小值是f[i - 1][1] + abs(A[i] - A'[j]); - 倒数第二个数选取的是
A'[2]的所有方案的结合，最小值是f[i - 1][2] + abs(A[i] - A'[j]); - …
- 倒数第二个数选取的是
A'[j]的所有方案的结合，最小值是f[i - 1][j] + abs(A[i] - A'[j]);
f[i][j]在所有子集的最小值中取min即可。
最终答案需要遍历最后一个数的所有取值，然后取min即可。
类似于AcWing 272. 最长公共上升子序列的优化方式，可以用前缀和思想优化掉一维循环。
时间复杂度
总共两重循环，时间复杂度是 $O(n^2)$。
C++ 代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 2010, INF = 0x3f3f3f3f;
int n;
int a[N], b[N];
int f[N][N];
int work()
{
for (int i = 1; i <= n; i ++ ) b[i] = a[i];
sort(b + 1, b + n + 1);
for (int i = 1; i <= n; i ++ )
{
int minv = INF;
for (int j = 1; j <= n; j ++ )
{
minv = min(minv, f[i - 1][j]);
f[i][j] = minv + abs(a[i] - b[j]);
}
}
int res = INF;
for (int i = 1; i <= n; i ++ ) res = min(res, f[n][i]);
return res;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
int res = work();
reverse(a + 1, a + n + 1);
res = min(res, work());
printf("%d\n", res);
return 0;
}
这不是蓝书的std吗？！/yiw
神仙打架，yxc和lyd大佬都选了这道题
初始红框内处在 [A_i, A_{i+1}]内的点怎么没有考虑？
会不会应该考虑的是A_i’和A_{i+1}’的中线上下的点？
感觉证明还是不太理解为什么一定能把所有的bi都移动到ai’上去。毕竟考虑每个位于 A′i,A’i+1,之间的一段的bi，不是最终的结果只是使得一个bi点ai’上了吗？怎么来的这一段bi的全部都在Ai‘’上呢
emmm我理解错了，现在我明白了。 由于每个位置的Ai是固定不变的，可能会大于Ai+1’,也可能会小于Ai’,所以我们可以把Ai’到Ai+1’这段区间的所有b都靠的尽可能离自己位置的Ai近一点，一定是边界之一。
写错了吧，“f[i][j] 代表所有给A[1] ~ A[i]分配好了值且最后一个B[i] = A’[j]的方案的集合；”，应该是给 B[1] - B[i] 分配好了值吧，或者说给 A[i] 对应的 B[i] 分配好了值（不然对于我这种萌新理解起来很难）
这也错了吧，前两行应该是 A’[1] 和 A’[2]
.... 看的真累
他是怎么保证b[i]选的时候是递增或递减的啊
minv=min{f[i-1][0],f[i-1][1],...,f[i - 1][j]}因为b数组排序了，上面的证明说是B一定是由A组成的，f[i,j]表示A的1~i安排完，最后一个选择为b[j]，每次都是从前往后选的
因为每次在算 f[i][j] 的时候，才进行minv=min(minv，f[i - 1][j])，那么此时的minv就是 第 i-1层中 以b[1]~b[j] 结尾的决策的集合里面的最小值。且b数组排过序。
因为每次在算 f[i][j] 的时候，才进行minv=min(minv，f[i - 1][j])，那么此时的minv就是 第 i-1层中 以b[1]~b[j] 结尾的决策的集合里面的最小值。且b数组排过序。
因为每次在算 f[i][j] 的时候，才进行minv=min(minv，f[i - 1][j])，那么此时的minv就是 第 i-1层中 以b[1]~b[j] 结尾的决策的集合里面的最小值。且b数组排过序。
因为每次在算 f[i][j] 的时候，才进行minv=min(minv，f[i - 1][j])，那么此时的minv就是 第 i-1层中 以b[1]~b[j] 结尾的决策的集合里面的最小值。且b数组排过序。
yxcnb！
您3个月前就吊打了现在的我orz
现在啥也不会
您7个月前就吊打了现在的我
$x$和$y$统计的应该是$A[k]$(k的下标区间在粉色框区间内)的数量吧，一开始没有想明白。
一个题解一大堆笔误，看的真心累。。。
这三个结论没想明白。绿色框框里的B上下移动，为什么要统计框框上和下的元素个数？框里的B上下移动只会影响与框里元素对应的A的差值大小。
如果将框整体上移 $d$ 的距离，那么总距离和增加 $y - x$；如果整体下移 $d$ 的距离，那么总距离和增加 $x - y$。所以你会发现增加的距离是与 $x$ 和 $y$ 相关的。
x和y应该说的是框里元素对应的A值吧
也可以考虑把整体一步一步的移动，设粉框中原序列a在下面的个数为x，在上面的个数为y，那么向上移动改变量为（x - y），向下移动改变量为（y - x），根据x，y大小关系我们可以一步步地移动，知道粉框的左边碰到下面或者粉框的右边碰到上面，那么我们就可以缩小粉框的范围继续求解了
其实如果是最优解进行改造的话，那么x = y是一定的（因为是最优解了），向上向下移动都可以
感觉应该是增加或减少$d(x-y)$吧
tql，感觉确实比书上的证明好懂一些。
很难不赞同
书上的感觉不严谨，就是有种怪怪的感觉
y老师，$B_i$ 是介于 $A’_i和和A’_{i+1}$，粉色框框中的 $B_i$ 中为何会有大于中为何会有大于 $A’_{i+1}$ 的数或者小于的数或者小于 $A’_i$ 的数？
大概懂了，是$B_i$对应的$A_i$ 跟$A_{i+1}’$ 和$A_i’$ 比较，而不是$B_i$自身跟$A_{i+1}’$ 和$A_i’$ 比较，ylstql。
对滴，$B_i$ 是 $A_i$ 变化之后的值，和 $A’_i$ 没啥关系。
Y总，我感觉这里通过巧妙地定义f[i][j]可以不需要前缀和。f[i][j]代表B到i这个index，A到j这个index的最小值（不用必须包括i）。这样的话，f[i][j] = min(f[i - 1][j], f[i][j - 1] + abs(A[i] - B[j])。这样的话可以直接取f[N][N]作为结果。
上面写错了，循环的时候可以从B的index作为外层循环，A作为里面。有点像背包问题的时候，巧妙地定义初值和集合的意义。
请问答案可能会爆int吗？
当 $\lbrace A_i \rbrace = \lbrace 10^9, -10^9, 10^9, -10^9, …\rbrace$ 这种交替序列时，答案会爆
int，因此在上面的代码中，最好使用long long类型的数组来保存状态。了解，谢谢啦。
这里一个A[i]是可以被用两次吗，也就是A和B数组不是一一对应的
对滴。
请问证明的时候B【i】是怎么被放上去的？
应该是假设的一组解
对滴，$B_i$ 是任意一组合法解。
老大，abs(a[i] - b[j])这里双重for循环的化取绝对值最小值不会都是0吗。。。为啥会不是，没大懂
这里会枚举到同一对数，但会被分摊到不同的
f[i][j]中，不能混在一起考虑。“闫氏DP分析法”是啥啊
y总自创的分析法，嘻嘻
这样啊Orz
就是从集合角度来分析DP问题，这里有个例子《算法竞赛进阶指南》0x51 线性DP。